Pre, Post and In-order Tree Traversal
Traversal
Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree −
- In-order Traversal
- Pre-order Traversal
- Post-order Traversal
Generally, we traverse a tree to search or locate a given item or key in the tree or to print all the values it contains.
Pre-order Traversal
In pre-order first visit Root node then visit left subtree and finally right subtree.
Root-Left-Right
Algorithm
Step 1: Visit root node. Step 2: Traverse left subtree(Recursively). Step 3: Traverse right subtree (Recursively).

Pre-order: abc Example:
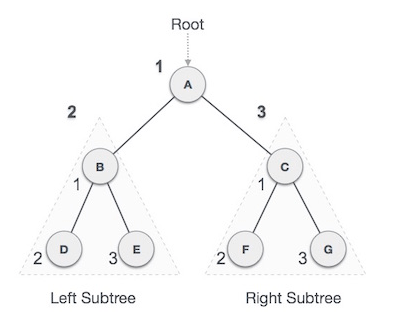
We first visit A the root node and then move to its left subtree B, B is also a root node of D&E so first print B then its left D and right E. The same is repeated for right sub tree C , C is root of F&G The process goes on until all the nodes are visited.
Pre-order: A → B → D → E → C → F → G
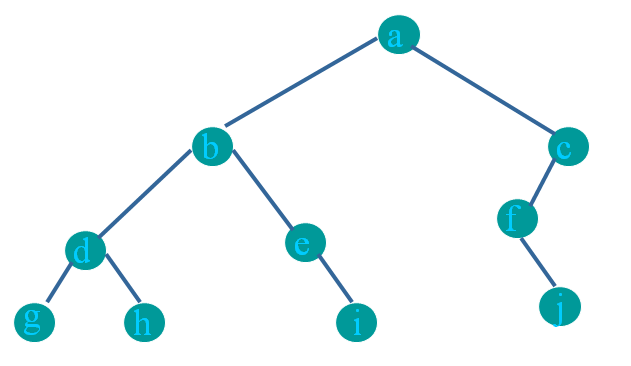
Example
Pre-order: abdgheicfj
Example
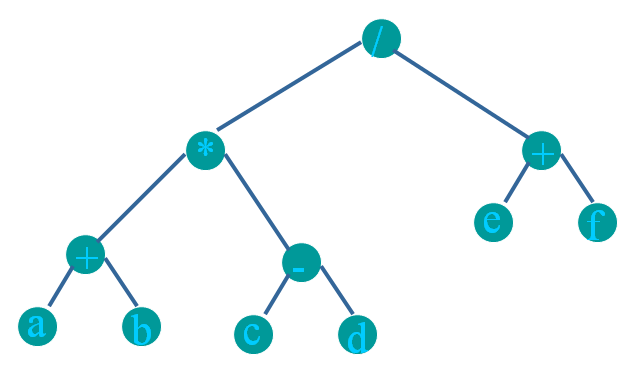
Pre-order:/*+ab-cd+ef
Pre-order traversal code
Void Preorder ( TreeNode <int> *treeNode )
{
if ( treeNode != Null)
{
Cout<< *(treeNode -> getInfo () ) << “ “;
Preorder ( treeNode -> getleft() );
Preorder (treeNode -> getRight() );
}
}
In-order Traversal
In this traversal method, the left subtree is visited first, then the root and later the right sub-tree.
Left-Root-Right
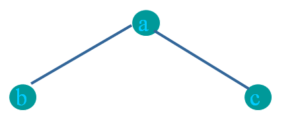
In-order: bac
Algorithm
Step 1: Traverse left subtree (Recursively). Step 2: Visit root node. Step 3: Traverse right subtree(Recursively).

We start from A, A is root so travers to left sub tree B, B is also a root of D&E again traverse to left. First print D then its root B and right E. DBand E is all left of Root A so after these print A and traverse right sub tree as same.
D → B → E → A → F → C → G
Example:

In-order traversal code
Void Inorder ( TreeNode <int> *treeNode )
{
if ( treeNode != Null)
{
Inorder ( treeNode -> getleft() );
Cout<< *(treeNode -> getInfo () ) << “ “;
Inorder (treeNode -> getRight() );
}
}
Postorder-order Traversal
First we traverse the left subtree, then the right subtree and finally the root node. Left-Right-Root

Postorder: bca
Algorithm
Step 1 − Traverse left subtree(Recursively). Step 2 − Traverse right subtree(Recursively). Step 3 − Visit root node.
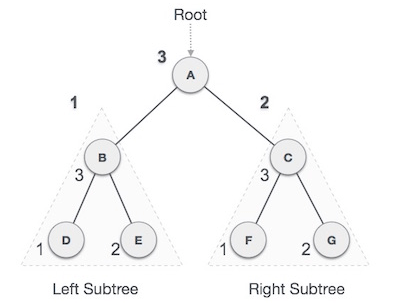
We start from A, and following Post-order traversal, we first visit the left subtree B. B is also traversed post-order. The process goes on until all the nodes are visited.
D → E → B → F → G → C → A
Example

Postorder: ab+cd-*ef+/
Postorder traversal code
Void Postorder ( TreeNode <int> *treeNode )
{
if ( treeNode != Null)
{
Postorder ( treeNode -> getleft() );
Postorder (treeNode -> getRight() );
Cout<< *(treeNode -> getInfo () ) << “ “;
}
}
Related links
Single link list Stack AVL Trees Binary search Counting Sort
Doubly link list Queue Graphs Bubble Sort Radix sort
Circular link list Binary search tree Hashing Insertion Sort Bucket Sort
Josephus Problem Tree Traversal Heaps Quick Sort Merge Sort
At Cui tutorial, courses, past papers and final year projects
#tutorial #cui #pastpaper #courses

