Binary Tree Complete code and application

Binary Tree is a special data structure used for data storage purposes. A binary tree has a special condition that each node can have a maximum of two children.

The following diagram represent tree

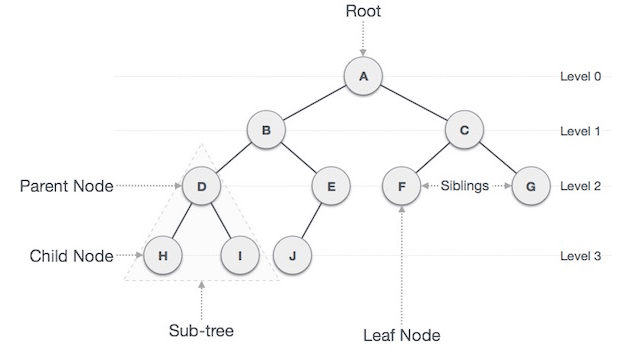
Important terms in tree

• Path − Path refers to the sequence of nodes along the edges of a tree.
• Root − The node at the top of the tree is called root. There is only one root per tree
• Parent − Any node except the root node has one edge upward to a node called parent.
• Child − The node below a given node connected by its edge downward is called its child node.
• Leaf − The node which does not have any child node is called the leaf node.
• Subtree − Subtree represents the descendants of a node.
• Visiting − Visiting refers to checking the value of a node when control is on the node.
• Traversing − Traversing means passing through nodes in a specific order.
• Levels − Level of a node represents the generation of a node. If the root node is at level 0, then its next child node is at level 1, its grandchild is at level 2, and so on.
• keys − Key represents a value of a node based on which a search operation is to be carried out for a node.

Binary Search Tree

Binary Search tree present the following behavior. A left node must have a value less than its parent’s value and right node child must have a value greater than its parent value.

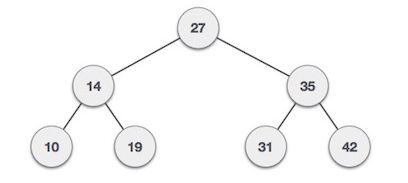
Tree Node

Tree node have the following three things

• Data
• Left pointer
• Right pointer

struct node {
   int data;   
   node *left;
   node *right;
};

Binary search tree basic 0perations

• Insert − Inserts an element in a tree/create a tree.
• Search − Searches an element in a tree.
• Preorder Traversal − Traverses a tree in a pre-order manner.
• Inorder Traversal − Traverses a tree in an in-order manner.
• Postorder Traversal − Traverses a tree in a post-order manner.

C++ code for Binary search tree

# include <iostream>
# include <cstdlib>
using namespace std;

struct node
{
int data;
node *left;
node *right;
}*root;

class BST
{
public:
int insert(node *, node *);
void preorder(node *);
void inorder(node *);
void postorder(node *);
void display(node *, int);
BST()
{
root = NULL;
}
};

int main()
{
int choice, num;
BST bst;
node *t;
while (1)
{
cout << “1.Insert Element ” << endl;
cout << “3.Inorder Traversal” << endl;
cout << “4.Preorder Traversal” << endl;
cout << “5.Postorder Traversal” << endl;
cout << “6.Display” << endl;
cout << “7.Quit” << endl<<endl;
cout << “Enter your choice : “;
cin >> choice;
switch (choice)
{
case 1:
t = new node;
cout << “Enter the number : “;
cin >> t->data;
bst.insert(root, t);
break;
case 3:
cout << “Inorder Traversal :” << endl;
bst.inorder(root);
cout << endl;
break;
case 4:
cout << “Preorder Traversal :” << endl;
bst.preorder(root);
cout << endl;
break;
case 5:
cout << “Postorder Traversal :” << endl;
bst.postorder(root);
cout << endl;
break;
case 6:
cout << “Display :” << endl;
bst.display(root, 1);
cout << endl;
break;
case 7:
exit(1);
default:
cout << “Wrong choice” << endl;
}
}
}

int BST::insert(node *q,node *newnode)
{
if (root == NULL)
{
root = new node;
root->data = newnode->data;
root->left = NULL;
root->right = NULL;
cout << “Root Node is Added” << endl<<endl;
return 0;
}
if (q->data == newnode->data)
{
cout << “Element already in the Tree” << endl;
return 0;
}
if (q->data > newnode->data)
{
if (q->left != NULL)
{
insert(q->left, newnode);
}
else
{
q->left = newnode;
(q->left)->left = NULL;
(q->left)->right = NULL;
cout << “Node Added To Left” << endl<<endl;
return 0;
}
}
else
{
if (q->right != NULL)
{
insert(q->right, newnode);
}
else
{
q->right = newnode;
(q->right)->left = NULL;
(q->right)->right = NULL;
cout << “Node Added To Right” << endl<<endl;
return 0;
}
}
}

void BST::preorder(node *q)
{
if (root == NULL)
{
cout << “q is empty” << endl;
return;
}
if (q != NULL)
{
cout << q->data << ” “;
preorder(q->left);
preorder(q->right);
}
}

void BST::inorder(node *q)
{
if (root == NULL)
{
cout << “q is empty” << endl;
return;
}
if (q != NULL)
{
inorder(q->left);
cout << q->data << ” “;
inorder(q->right);
}
}

void BST::postorder(node *q)
{
if (root == NULL)
{
cout << “q is empty” << endl;
return;
}
if (q != NULL)
{
postorder(q->left);
postorder(q->right);
cout << q->data << ” “;
}
}

void BST::display(node *q, int level)
{
int i;
if (q != NULL)
{
display(q->right, level + 1);
cout << endl;
if (q == root)
cout << “Root->: “;
else
{
for (i = 0; i < level; i++)
cout << ” “;
}
cout << q->data;
display(q->left, level + 1);
}
}

 

Related links 

Single link list                 Stack              AVL Trees             Binary search          Counting Sort

Doubly link list               Queue              Graphs                  Bubble Sort               Radix sort

Circular link list              Binary search tree       Hashing         Insertion Sort         Bucket Sort

Josephus Problem          Tree Traversal              Heaps                Quick Sort              Merge Sort

 

At Cui tutorial, courses, past papers and final year projects

#tutorial #cui #pastpaper #courses