AVL Trees
Activity Outcomes:
This lab teaches you the following topics:
- How to insert and delete data from AVL trees
- How to search and traverse AVL trees
Introduction
AVL Tree:
AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes.
An Example Tree that is an AVL Tree

The above tree is AVL because differences between heights of left and right subtrees for every node is less than or equal to 1.
An Example Tree that is NOT an AVL Tree
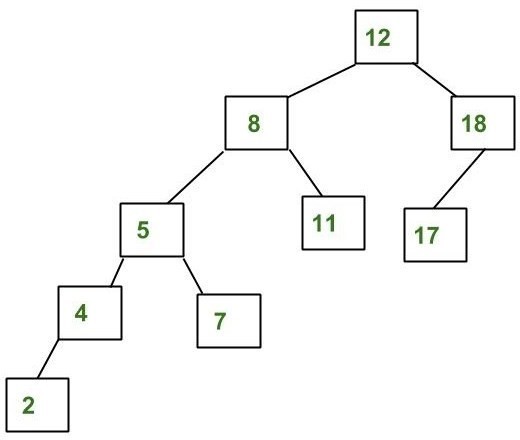
The above tree is not AVL because differences between heights of left and right subtrees for 8 and 18 is greater than 1.
Why AVL Trees?
Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that height of the tree remains O(Logn) after every insertion and deletion, then we can guarantee an upper bound of O(Logn) for all these operations. The height of an AVL tree is always O(Logn) where n is the number of nodes in the tree.
Lab Activities:
Activity 1:
Write a program to insert a node in AVL tree while balancing.
Solution:
// C program to insert a node in AVL tree
#include<stdio.h>
#include<stdlib.h>
// An AVL tree node
struct Node
{
int key;
struct Node *left;
struct Node *right;
int height;
};
// A utility function to get maximum of two integers
int max(int a, int b);
// A utility function to get the height of the tree
int height(struct Node *N)
{
if (N == NULL)
return 0;
return N->height;
}
// A utility function to get maximum of two integers
int max(int a, int b)
{
return (a > b)? a : b;
}
/* Helper function that allocates a new node with the given key and NULL left and right pointers. */
struct Node* newNode(int key)
{
struct Node* node = (struct Node*)malloc(sizeof(struct Node));
node->key = key;
node->left = NULL;
node->right = NULL;
node->height = 1; // new node is initially added at leaf return(node);
}
// A utility function to right rotate subtree rooted with y , See the diagram given above.
struct Node *rightRotate(struct Node *y)
{
struct Node *x = y->left;
struct Node *T2 = x->right;
// Perform rotation
x->right = y;
y->left = T2;
// Update heights
y->height = max(height(y->left), height(y->right))+1;
x->height = max(height(x->left), height(x->right))+1;
// Return new root
return x;
}
// A utility function to left rotate subtree rooted with x, See the diagram given above.
struct Node *leftRotate(struct Node *x)
{
struct Node *y = x->right;
struct Node *T2 = y->left;
// Perform rotation
y->left = x;
x->right = T2;
// Update heights
x->height = max(height(x->left), height(x->right))+1;
y->height = max(height(y->left), height(y->right))+1;
// Return new root
return y;
}
// Get Balance factor of node N
int getBalance(struct Node *N)
{
if (N == NULL)
return 0;
return height(N->left) – height(N->right);
}
// Recursive function to insert a key in the subtree rooted with node and returns the new root of the subtree.
struct Node* insert(struct Node* node, int key)
{
/* 1. Perform the normal BST insertion */
if (node == NULL)
return(newNode(key));
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
else // Equal keys are not allowed in BST
return node;
/* 2. Update height of this ancestor node */
node->height = 1 + max(height(node->left),
height(node->right));
/* 3. Get the balance factor of this ancestor node to check whether this node became unbalanced */
int balance = getBalance(node);
// If this node becomes unbalanced, then there are 4 cases
// Left Left Case
if (balance > 1 && key < node->left->key)
return rightRotate(node);
// Right Right Case
if (balance < -1 && key > node->right->key)
return leftRotate(node);
// Left Right Case
if (balance > 1 && key > node->left->key)
{
node->left = leftRotate(node->left);
return rightRotate(node);
}
// Right Left Case
if (balance < -1 && key < node->right->key)
{
node->right = rightRotate(node->right);
return leftRotate(node);
}
/* return the (unchanged) node pointer */
return node;
}
// A utility function to print preorder traversal of the tree.
// The function also prints height of every node
void preOrder(struct Node *root)
{
if(root != NULL)
{
printf(“%d “, root->key);
preOrder(root->left);
preOrder(root->right);
}
}
/* Drier program to test above function*/
int main()
{
struct Node *root = NULL;
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 30);
root = insert(root, 40);
root = insert(root, 50);
root = insert(root, 25);
/* The constructed AVL Tree would be
30
/ \
20 40
/ \ \
10 25 50
*/
printf(“Preorder traversal of the constructed AVL” ” tree is \n”);
preOrder(root);
return 0;
}
Activity 2:
Write a function to delete a node from an AVL tree and display the updated tree.
Solution:
// C program to delete a node from AVL Tree
#include<stdio.h>
#include<stdlib.h>
// An AVL tree node
struct Node
{
int key;
struct Node *left;
struct Node *right;
int height;
};
// A utility function to get maximum of two integers
int max(int a, int b);
// A utility function to get height of the tree
int height(struct Node *N)
{
if (N == NULL)
return 0;
return N->height;
}
// A utility function to get maximum of two integers
int max(int a, int b)
{
return (a > b)? a : b;
}
/* Helper function that allocates a new node with the given key and NULL left and right pointers. */
struct Node* newNode(int key)
{
struct Node* node = (struct Node*)malloc(sizeof(struct Node));
node->key = key;
node->left = NULL;
node->right = NULL;
node->height = 1; // new node is initially added at leaf
return(node);
}
// A utility function to right rotate subtree rooted with y
// See the diagram given above.
struct Node *rightRotate(struct Node *y)
{
struct Node *x = y->left;
struct Node *T2 = x->right;
// Perform rotation
x->right = y;
y->left = T2;
// Update heights
y->height = max(height(y->left), height(y->right))+1;
x->height = max(height(x->left), height(x->right))+1;
// Return new root
return x;
}
// A utility function to left rotate subtree rooted with x
// See the diagram given above.
struct Node *leftRotate(struct Node *x)
{
struct Node *y = x->right;
struct Node *T2 = y->left;
// Perform rotation
y->left = x;
x->right = T2;
// Update heights
x->height = max(height(x->left), height(x->right))+1;
y->height = max(height(y->left), height(y->right))+1;
// Return new root
return y;
}
// Get Balance factor of node N
int getBalance(struct Node *N)
{
if (N == NULL)
return 0;
return height(N->left) – height(N->right);
}
struct Node* insert(struct Node* node, int key)
{
/* 1. Perform the normal BST rotation */
if (node == NULL)
return(newNode(key));
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
else // Equal keys not allowed
return node;
/* 2. Update height of this ancestor node */
node->height = 1 + max(height(node->left),height(node->right));
/* 3. Get the balance factor of this ancestor node to check whether this node became unbalanced */
int balance = getBalance(node);
// If this node becomes unbalanced, then there are 4 cases
// Left Left Case
if (balance > 1 && key < node->left->key)
return rightRotate(node);
// Right Right Case
if (balance < -1 && key > node->right->key)
return leftRotate(node);
// Left Right Case
if (balance > 1 && key > node->left->key)
{
node->left = leftRotate(node->left);
return rightRotate(node);
}
// Right Left Case
if (balance < -1 && key < node->right->key)
{
node->right = rightRotate(node->right);
return leftRotate(node);
}
/* return the (unchanged) node pointer */
return node;
}
/* Given a non-empty binary search tree, return the node with minimum key value found in that tree. Note that the entire tree does not need to be searched. */
struct Node * minValueNode(struct Node* node)
{
struct Node* current = node;
/* loop down to find the leftmost leaf */
while (current->left != NULL)
current = current->left;
return current;
}
// Recursive function to delete a node with given key from subtree with given root. It returns root of the modified subtree.
struct Node* deleteNode(struct Node* root, int key)
{
// STEP 1: PERFORM STANDARD BST DELETE
if (root == NULL)
return root;
// If the key to be deleted is smaller than the root’s key, then it lies in left subtree
if ( key < root->key )
root->left = deleteNode(root->left, key);
// If the key to be deleted is greater than the root’s key, then it lies in right subtree
else if( key > root->key )
root->right = deleteNode(root->right, key);
// if key is same as root’s key, then This is the node to be deleted
else
{
// node with only one child or no child
if( (root->left == NULL) || (root->right == NULL) )
{
struct Node *temp = root->left ? root->left :root->right;
// No child case
if (temp == NULL)
{
temp = root;
root = NULL;
}
else // One child case
*root = *temp; // Copy the contents of the non-empty child
free(temp);
}
else
{
// node with two children: Get the inorder successor (smallest in the right subtree)
struct Node* temp = minValueNode(root->right);
// Copy the inorder successor’s data to this node
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->key);
}
}
// If the tree had only one node then return
if (root == NULL)
return root;
// STEP 2: UPDATE HEIGHT OF THE CURRENT NODE
root->height = 1 + max(height(root->left),
height(root->right));
// STEP 3: GET THE BALANCE FACTOR OF THIS NODE (to check whether this node became unbalanced)
int balance = getBalance(root);
// If this node becomes unbalanced, then there are 4 cases
// Left Left Case
if (balance > 1 && getBalance(root->left) >= 0)
return rightRotate(root);
// Left Right Case
if (balance > 1 && getBalance(root->left) < 0)
{
root->left = leftRotate(root->left);
return rightRotate(root);
}
// Right Right Case
if (balance < -1 && getBalance(root->right) <= 0)
return leftRotate(root);
// Right Left Case
if (balance < -1 && getBalance(root->right) > 0)
{
root->right = rightRotate(root->right);
return leftRotate(root);
}
return root;
}
// A utility function to print preorder traversal of the tree.
// The function also prints height of every node
void preOrder(struct Node *root)
{
if(root != NULL)
{
printf(“%d “, root->key);
preOrder(root->left);
preOrder(root->right);
}
}
/* Driver program to test above function*/
int main()
{
struct Node *root = NULL;
root = insert(root, 9);
root = insert(root, 5);
root = insert(root, 10);
root = insert(root, 0);
root = insert(root, 6);
root = insert(root, 11);
root = insert(root, -1);
root = insert(root, 1);
root = insert(root, 2);
/* The constructed AVL Tree would be
9
/ \
1 10
/ \ \
0 5 11
/ / \
-1 2 6
*/
printf(“Preorder traversal of the constructed AVL ” “tree is \n”);
preOrder(root);
root = deleteNode(root, 10);
/* The AVL Tree after deletion of 10
1
/ \
0 9
/ / \
-1 5 11
/ \
2 6
*/
printf(“\nPreorder traversal after deletion of 10 \n”);
preOrder(root);
return 0;
}
Activity 3:
Write a function to search in AVL tree.
Solution:
Algorithm Search(x, root)
{
if(tree is empty ) then print “tree is empty”
otherwise
If(x grater than root) search(root-right);
Otherwise if(x less than root ) search(root-left)
Otherwise return true
}
}
int avltree[40],t=1,s,x,i;
void insert(int,int );
int search1(int,int);
void main()
{
Insert(root, 9);
Insert(root. 7);
Search1(root,7);
}
void insert(int s,int ch )
{
int x,y;
if(t==1)
{
avltree[t++]=ch;
return;
}
x=search1(s,ch);
if(avltree[x]>ch)
{
avltree[2*x]=ch;
y=log(2*x)/log(2);
if(height(1,y))
{
if( x%2==0 )
update1();
else
update2();
}
}
else {
avltree[2*x+1]=ch;
y=log(2*x)/log(2);
if(height(1,y))
{ if(x%2==1)
update1();
else
update2();
}
}
t++;
}
int search1(int s,int ch)
{
if(t==1)
{
cout <<“no element in avltree”; return -1;
}
if(avltree[s]==-1)
return s/2;
if(avltree[s] > ch)
search1(2*s,ch);
else
search1(2*s+1,ch);
}
int height(int s,int y)
{
if(avltree[s]==-1)
return;
}
Home Activities:
- Search the minimum number in AVL tree
- Search the maximum number in the AVL tree
- Search the minimum subtree in the AVL tree
- Write a program to insert data in Red Black
- Write a program to delete a node from red black trees and display the tree in post
- Write a program to search an element in red black trees.
Related links
Single link list Stack AVL Trees Binary search Counting Sort
Doubly link list Queue Graphs Bubble Sort Radix sort
Circular link list Binary search tree Hashing Insertion Sort Bucket Sort
Josephus Problem Tree Traversal Heaps Quick Sort Merge Sort
At Cui tutorial, courses, past papers and final year projects
#tutorial #cui #pastpaper #courses

