QUEUE complete code using array and link list and real life application and its operation
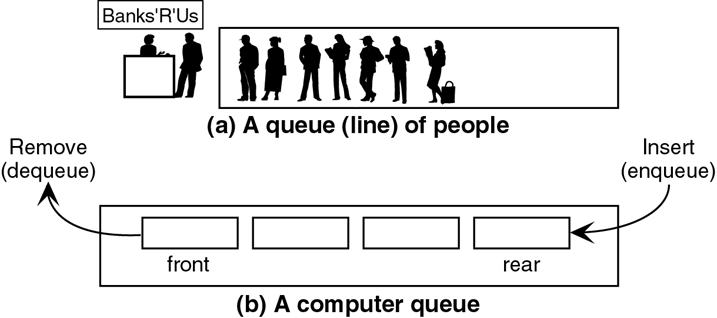
A queue is an ordered collection of items from which items may be deleted at one end (called the front of the queue) and into which items may be inserted at the other end (called the rear of the queue)
Data structure which implements a first-in, first-out list; e.g. print queue, which contains a list of jobs to be printed in order.
In programming, a queue is a data structure in which elements are removed in the same order they were entered. This is often referred to as FIFO (first in, first out).
In the queue, as in the stack, all deletions occur at the head of the list. However, all insertions to the queue occur at the tail of the list.
APPLICATIONS
- Ticketing counter
- Bus stop line
- Bank Customers
- Printer SPOOL
- CPU Scheduling (at times)
- Etc etc etc
QUEUE OPERATIONS
- Determine whether or not if the queue Q is empty.
- Determine whether or not if the queue Q is full.
- Insert (enqueue) a new item onto the rear of the queue Q.
- Remove (dequeue) an item from the front of Q, provided Q is nonempty.
- isEmpty() – check to see if the queue is empty.
- isFull() – check to see if the queue is full.
- enqueue(element) – put the element at the end of the queue.
- dequeue() – take the first element from the queue.
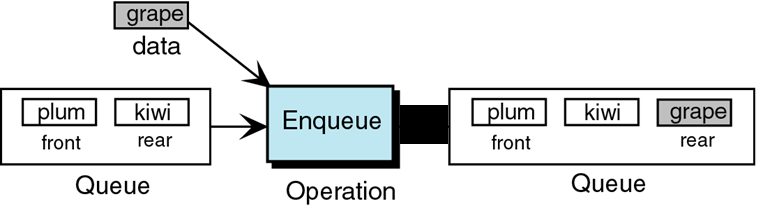
ENQUEUE
The queue insert is known as enqueue.
After the data has been inserted, this new element becomes the rear of the queue.
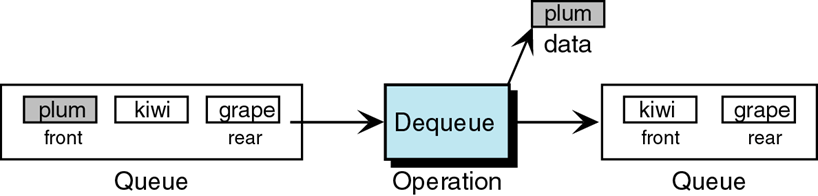
DEQUEUE
The queue delete operation is known as dequeue.
The data at the front of the queue is returned to the user and deleted from the queue.
Queue Using linklist
#include “stdafx.h”
#include<iostream>
#include<cstdlib>
using namespace std;
struct node
{
int data;
struct node *link;
}*p, *r;
class queue_list
{
public:
void insert(int);
void display();
void del();
queue_list()
{
p = NULL;
r = NULL;
}
};
int main()
{
int choice, x;
queue_list ql;
while (1)
{
cout << “\n” << endl;
cout << “1.Insert Element into the Queue” << endl;
cout << “2.Delete Element from the Queue” << endl;
cout << “3.Display the Queue” << endl;
cout << “4.Quit” << endl;
cout << “Enter your Choice: “;
cin >> choice;
switch (choice)
{
case 1:
cout << “Enter the value to insert: “;
cin >> x;
ql.insert(x);
break;
case 2:
ql.del();
break;
case 3:
ql.display();
break;
case 4:
exit(1);
break;
default:
cout << “Wrong Choice” << endl;
}
}
return 0;
}
void queue_list::insert(int x)
{
node *t;
t = new (struct node);
t->data = x;
t->link = NULL;
if (p == NULL)
p = t;
r=t;
else
r->link = t;
r = t;
}
void queue_list::del()
{
node *q;
if (p == NULL)
cout << “Queue Underflow” << endl;
else
{
q= p;
cout << “Element Deleted: ” << q->data << endl;
p = p->link;
free(q);
}
}
void queue_list::display()
{
node *q;
q = p;
if (p == NULL)
cout << “Queue is empty” << endl;
else
{
cout << “Queue elements :” << endl;
while (q != NULL)
{
cout << q->data << ” “;
q = q->link;
}
cout << endl;
}
}
Queue Using Array
#include <iostream>
#include <conio.h>
using namespace std;
class queue
{
int qu[5];
int front;
int rear;
public:
queue()
{
front = -1;
rear = -1;
}
void insert(int x)
{
if (front == – 1)
front = 0;
if (rear>4)
cout<<“\nQueue Overflow”<<endl;
else
qu[++rear] = x;
}
void dequeue()
{
if (front == -1 || front > rear)
{
cout<<“\nQueue Underflow “;
return ;
}
else
{
cout<<“\nElement deleted from queue is : “<< qu[front++] <<endl;
}
}
void display()
{
if (front == -1)
cout<<“\nQueue is empty”<<endl;
else
{
cout<<“\nQueue elements are : “;
for (int i = front; i <= rear; i++)
cout<<qu[i]<<” “;
cout<<endl;
}
}
}; // End Class
int main()
{
int ch,val;
queue q;
do
{
cout<<“\n1) Insert element to queue”<<endl;
cout<<“2) Delete element from queue”<<endl;
cout<<“3) Display all the elements of queue”<<endl;
cout<<“4) Exit”<<endl;
cout<<“\nEnter your choice : “<<endl;
cin>>ch;
switch (ch)
{
case 1:
cout<<“\nInsert the element in queue : “<<endl;
cin>>val;
q.insert(val);
break;
case 2:
q.dequeue();
break;
case 3:
cout<<endl;
q.display();
cout<<endl;
break;
case 4:
cout<<“\nExit”<<endl;
break;
default:
cout<<“\nInvalid choice”<<endl;
}
} while(ch!=4);
return 0;
}
Related links
Single link list Stack AVL Trees Binary search Counting Sort
Doubly link list Queue Graphs Bubble Sort Radix sort
Circular link list Binary search tree Hashing Insertion Sort Bucket Sort
Josephus Problem Tree Traversal Heaps Quick Sort Merge Sort
At Cui tutorial, courses, past papers and final year projects
#tutorial #cui #pastpaper #courses

