Stack Complete Code and Application

Stack Data Structure complete code using Array and link list

and its application,

A stack is an ordered collection of items into which new items may be inserted and from which items may be deleted at one end called the TOP of the stack

What are the properties of these stacks?

You can only add an item (book shirt etc) on top of the stack and you can only remove it from the top too

BASIC OPERATIONS WITH STACKS

Push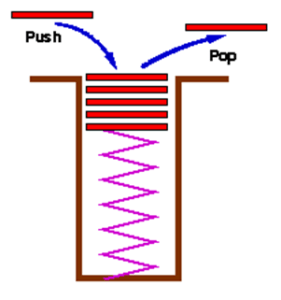

🞤 Add and item

🞫 need to check overflow

Pop

🞤 Remove an item

🞫 need to check underflow

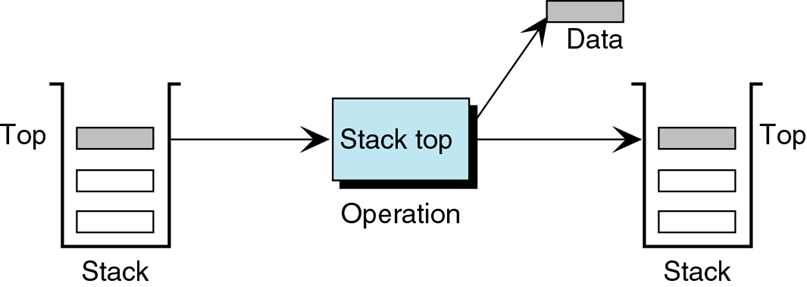
stackTop

🞤 What’s on the Top

🞫 Could be empty

Push

Adds a new data element to the top of the stack
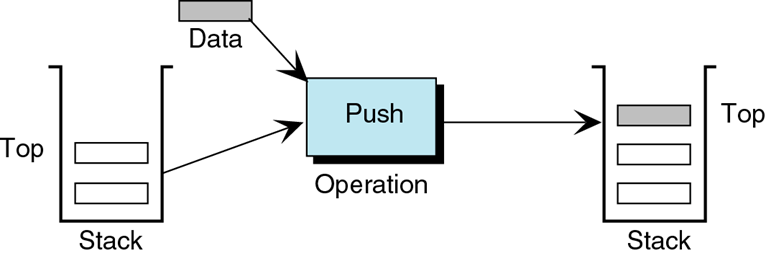
Stack Push Method

Pop

Removes a data element from the top of the stack

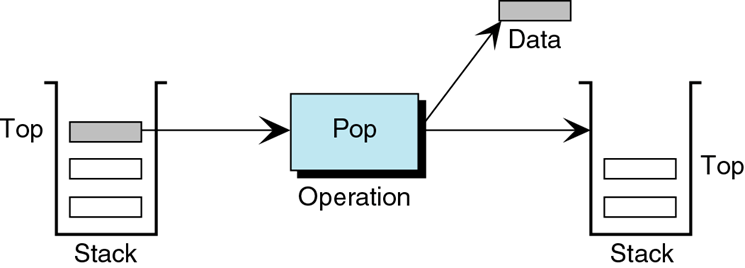
Stack Data structure — pop method in stack

StackTop

Checks the top Stack is not changed

Stacks in real life: stack of books, stack of plates

Add new items at the top
Remove an item at the top
Stack data structure similar to real life: collection of elements arranged in a linear order.

Can only access element at the top
A stack is an ordered collection of items into which new items may be inserted and from which items may be deleted at one end only, called top of the stack. i.e. deletion/insertion can only be done from top of the stack
The insert operation on a stack is often called Push operation and delete operation is called Pop operation.

OPERATION ON STACK

A Stack should have the following methods

push(item) //Push an item onto the stack
pop( ) //Pop an item off the stack

isEmpty() //Return true if stack is empty.
Isfull( ) //Return true if stack is full

Basic operation code

Stack by using an Array

#include “stdafx.h”
#include<iostream>
#include<conio.h>
#include<stdlib.h>
using namespace std;
class stack
{
int stk[5];
int top;
public:
stack()
{
top = -1;
}
void push(int x)
{
if (top > 4)
{
cout << “stack over flow”;
return;
}
stk[++top] = x;
cout << “inserted” << x << endl;
}
void pop()
{
if (top <0)
{
cout << “stack under flow”;
return;
}
cout << “deleted” << stk[top–];
}
void display()
{
if (top<0)
{
cout << ” stack empty”;
return;
}
for (int i = top; i >= 0; i–)
cout << stk[i] << ” “;
}
};

int main()
{
int ch;
stack st;
while (1)
{
cout << “\n1.push \n2.pop \n3.display \n4.exit\n\nEnter ur choice”;
cin >> ch;
switch (ch)
{
case 1: cout << “enter the element”;
cin >> ch;
st.push(ch);
break;
case 2: st.pop(); break;
case 3: st.display(); break;
case 4: exit(0);
}
}
return (0);

}

Stack by using linklist

#include “stdafx.h”
#include <iostream>
#include <stdio.h>
#include <conio.h>
using namespace std;
struct node
{
int data;
node *next;
}*p = NULL, *r = NULL, *q = NULL, *t = NULL;
void push(int x)
{
t = new node;
t->data = x;
t->next = NULL;
if (p == NULL)
{
p = t;

}
else
{
t->next = p;
p = t;

}
}
int pop()
{
int x;
if (p == NULL)
{
cout << “emqty queue\n”;
}
else
{
q = p;
x = q->data;
p = p->next;
delete(q);
return(x);
}
}
int main()
{
/*int n, c = 0, x;
cout << “Enter the number of values to be qushed into stack\n”;
cin >> n;
while (c < n)
{
cout << “Enter the value to be entered into queue = “;
cin >> x;
push(x);
c++;
}
cout << “\n\nRemoved Values\n\n”;
while (true)
{
if (p != NULL)
cout << remove() << endl;
else
break;
}

//write system pause command here

int ch;
while (1)
{
cout << “\n1.push \n2.pop \n3.exit\n\nEnter ur choice”;
cin >> ch;
switch (ch)
{
case 1: cout << “enter the element”;
cin >> ch;
push(ch);
break;
case 2: pop(); break;

case 3: exit(0);
}
}
return (0);
}

How to access the top of the stack
How to push data onto the stack
How to pop data from the stack

At Cui tutorial, courses, past papers and final year projects

#tutorial #cui #pastpaper #courses