Merge Sort

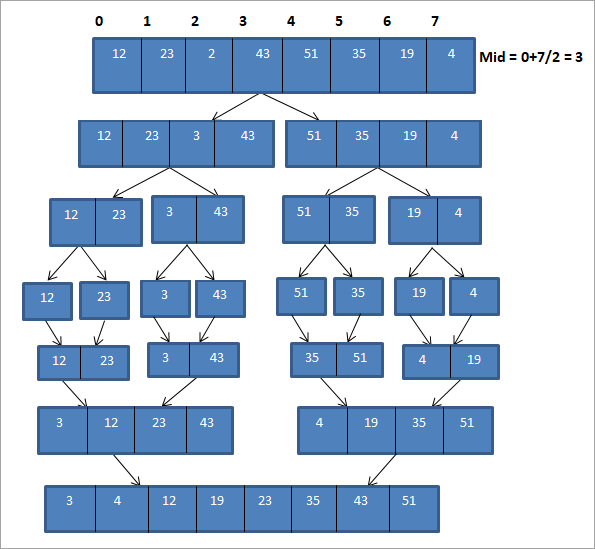
• Divide and conquer approach
• Merging is process of combining two sorted files into a third sorted file
• Given two sorted arrays A and B each of size k/2, merge them into an array C of size k. Array C should also be sorted
• Here we are going to merge two pre-sorted arrays

void MergeSort(int A[],int lower,int upper)

{

if (lower==upper)

return;

int middle=(lower+upper)/2;

MergeSort(A,lower,middle);

MergeSort(A,middle+1,upper);

MergeArray(A,lower,middle,middle+1,upper);

}

void MergeArray(int A[],int lower1,int upper1,int lower2,int upper2)

{

int size=(upper1-lower1+1) + (upper2-lower2+1);

int i,j,k,*C=new int[size];

for(i=0,j=lower1,k=lower2;j<=upper1 && k<=upper2;i++)

if(A[j]<=A[k])  C[i]=A[j++];

else C[i]=A[k++];

while(j<=upper1)  C[i++]=A[j++];

while(k<=upper2)  C[i++]=A[k++];

j=(lower1<lower2)?lower1:lower2;

for(i=0;i<size;i++,j++)

A[j]=C[i];

}

Time Complexity

• Recurrence relation
• T(n)=2T(n/2)+n

C++ code for merge sort

#include<iostream>
#include<conio.h>
#include<cstdlib>
#include<time.h>

using namespace std;

void merge(int a[],int low,int mid,int high)
{
int h,i,j,b[50],k;
h=low;
i=low;
j=mid+1;

while(h<=mid&&j<=high)
{
if(a[h]<=a[j])
{
b[i]=a[h];
h++;
}
else
{
b[i]=a[j];
j++;
}
i++;
}
if(h>mid)
{
for(k=j;k<=high;k++)
{
b[i]=a[k];
i++;
}
}
else
{
for(k=h;k<=mid;k++)
{
b[i]=a[k];
i++;
}
}
for(k=low;k<=high;k++) a[k]=b[k];
}

void merge_sort(int a[],int left, int right)
{
if(left-right!=0)
{
int mid=(left+right)/2;
merge_sort(a,left,mid);
merge_sort(a,mid+1,right);
merge(a,left,mid,right);
}
}

int main()
{
srand(time(0));
int a[10];

for(int i=0;i<=9;i++)
a[i]=rand()%100;
for(int i=0;i<=9;i++)
cout<<a[i]<<” “;
cout<<endl;
merge_sort(a,0,9);
for(int i=0;i<=9;i++)
cout<<a[i]<<” “;

getch();
}

C++ code for merge sort using class

#include <iostream.h>
const int MAX = 5 ;
class array
{
private :
int *a ;
int size ;
int count ;
public :
array( ) ;
array ( int sz ) ;
void add ( int num ) ;
void display( ) ;
void merge_sort(int low,int high);
void merge(int low,int mid,int high);
~array( ) ;
} ;
array :: array( )
{
count = size = 0 ;
a = NULL ;
}
array :: array( int sz )
{
count = 0 ;
size = sz ;
a = new int[sz] ;
}
void array :: add ( int num )
{
if ( count < size )
{
a[count] = num ;
count++ ;
}
else
cout << “\nArray is full” << endl ;
}
void array :: display( )
{
for ( int i = 0 ; i < count ; i++ )
cout << a[i] << “\t” ;
cout << endl ;
}
void array :: merge_sort(int low,int high)
{

int mid;
if(low<high)
{
mid=(low+high)/2;
merge_sort(low,mid);
merge_sort(mid+1,high);
merge(low,mid,high);
}
}
void array :: merge(int low,int mid,int high)
{
int h,i,j,b[50],k;
h=low;
i=low;
j=mid+1;

while((h<=mid)&&(j<=high))
{
if(a[h]<=a[j])
{
b[i]=a[h];
h++;
}
else
{
b[i]=a[j];
j++;
}
i++;
}
if(h>mid)
{
for(k=j;k<=high;k++)
{
b[i]=a[k];
i++;
}
}
else
{
for(k=h;k<=mid;k++)
{
b[i]=a[k];
i++;
}
}
for(k=low;k<=high;k++) a[k]=b[k];
}
array :: ~array( )
{
delete a ;
}

void main( )
{
array a ( MAX ) ;

a.add ( 11 ) ;
a.add ( 2 ) ;
a.add ( 9 ) ;
a.add ( 13 ) ;
a.add ( 57 ) ;
cout << “\nMerge sort.\n” ;
a.merge_sort (0,4) ;
cout << “\nArray after sorting: ” << endl ;
a.display( ) ;
}

Related links 

Single link list                 Stack              AVL Trees             Binary search          Counting Sort

Doubly link list               Queue              Graphs                  Bubble Sort               Radix sort

Circular link list              Binary search tree       Hashing         Insertion Sort         Bucket Sort

Josephus Problem          Tree Traversal              Heaps                Quick Sort              Merge Sort

 

At Cui tutorial, courses, past papers and final year projects

#tutorial #cui #pastpaper #courses