Traversal

Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree −

• In-order Traversal
• Pre-order Traversal
• Post-order Traversal

Generally, we traverse a tree to search or locate a given item or key in the tree or to print all the values it contains.

Pre-order Traversal

In pre-order first visit Root node then visit left subtree and finally right subtree.

Root-Left-Right

Algorithm

Step 1: Visit root node.
Step 2: Traverse left subtree(Recursively).
Step 3: Traverse right subtree (Recursively).

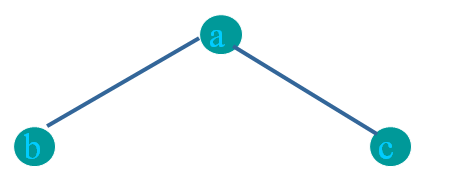
Pre-order: abc
Example:

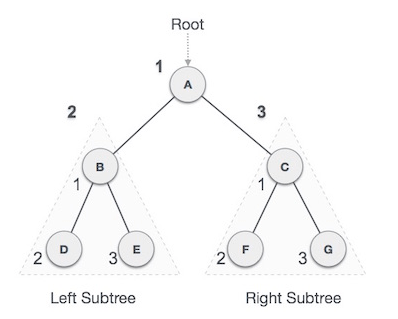
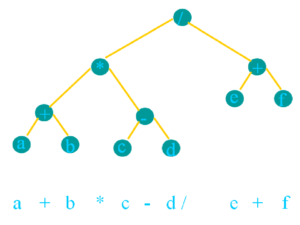
We first visit A the root node and then move to its left subtree B,  B is also a root node of D&E so first print B then its left D and right E.  The same is repeated for right sub tree C , C is root of F&G The process goes on until all the nodes are visited.

Pre-order: A → B → D → E → C → F → G

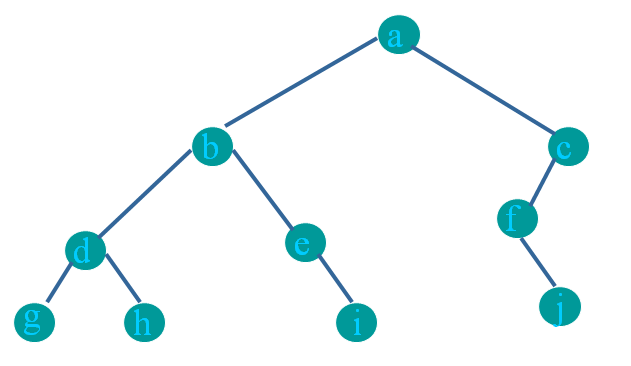
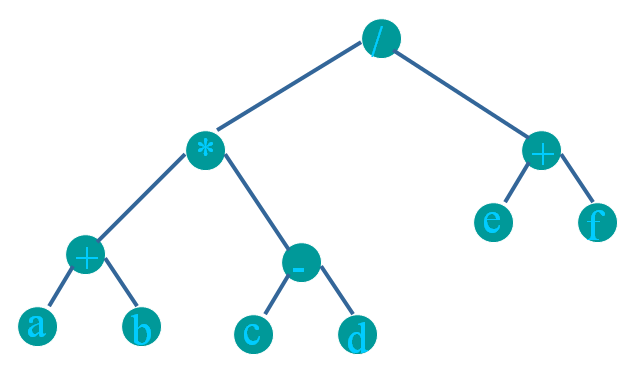
Example

Pre-order: abdgheicfj
Example

Pre-order:/*+ab-cd+ef

Pre-order traversal code

Void Preorder ( TreeNode <int> *treeNode )

{

if ( treeNode != Null)

{

Cout<< *(treeNode -> getInfo () ) << “  “;

Preorder ( treeNode -> getleft() );

Preorder (treeNode -> getRight() );

}

}

In-order Traversal

In this traversal method, the left subtree is visited first, then the root and later the right sub-tree.

Left-Root-Right

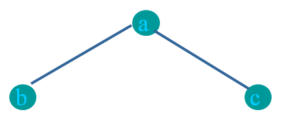
In-order: bac

Algorithm

Step 1: Traverse left subtree (Recursively).
Step 2: Visit root node.
Step 3: Traverse right subtree(Recursively).

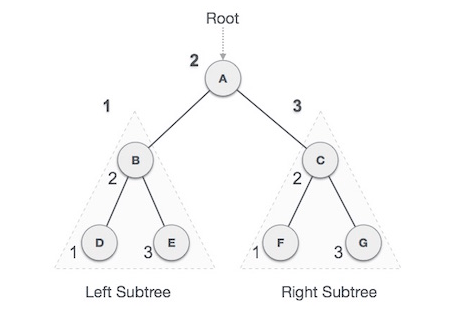
We start from A, A is root so travers to left sub tree B, B is also a root of D&E again traverse to left. First print D then its root B and right E.  DBand E is all left of Root A so after these print A and traverse right sub tree as same.

D → B → E → A → F → C → G

Example:

In-order traversal code

Void Inorder ( TreeNode <int> *treeNode )

{

if ( treeNode != Null)

{

Inorder ( treeNode -> getleft() );

Cout<< *(treeNode -> getInfo () ) << “  “;

Inorder (treeNode -> getRight() );

}

}

Postorder-order Traversal

First we traverse the left subtree, then the right subtree and finally the root node. Left-Right-Root

Postorder: bca

Algorithm

Step 1 − Traverse left subtree(Recursively).
Step 2 − Traverse right subtree(Recursively).
Step 3 − Visit root node.

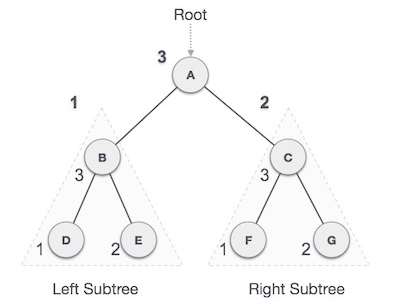
We start from A, and following Post-order traversal, we first visit the left subtree B. B is also traversed post-order. The process goes on until all the nodes are visited.

D → E → B → F → G → C → A

Example

Postorder: ab+cd-*ef+/

Postorder traversal code

Void Postorder ( TreeNode <int> *treeNode )

{

if ( treeNode != Null)

{

Postorder ( treeNode -> getleft() );

Postorder (treeNode -> getRight() );

Cout<< *(treeNode -> getInfo () ) << “  “;

}

}

 

Related links 

Single link list                 Stack              AVL Trees             Binary search          Counting Sort

Doubly link list               Queue              Graphs                  Bubble Sort               Radix sort

Circular link list              Binary search tree       Hashing         Insertion Sort         Bucket Sort

Josephus Problem          Tree Traversal              Heaps                Quick Sort              Merge Sort

 

At Cui tutorial, courses, past papers and final year projects

#tutorial #cui #pastpaper #courses