Quick Sort
Quick Sort
Quick Sort : Based on Divide and Conquer paradigm.
- One of the fastest in-memory sorting algorithms (if not the fastest)
- is a very efficient sorting algorithm
- designed by C.A.R.Hoare in 1960.
- Consists of two phases:
- Partition phase
- Sort phase
Steps…
- Divide: Pick a pivot element and rearrange the array so that
– all elements to the left of the pivot are
smaller than the pivot.
– all elements to the right of the pivot are larger
than the pivot.
- Conquer: Recursively quicksort the left and right subarrays.
3:Combine: since subarrays are sorted in place, no work is needed to combine them, array is now sorted.
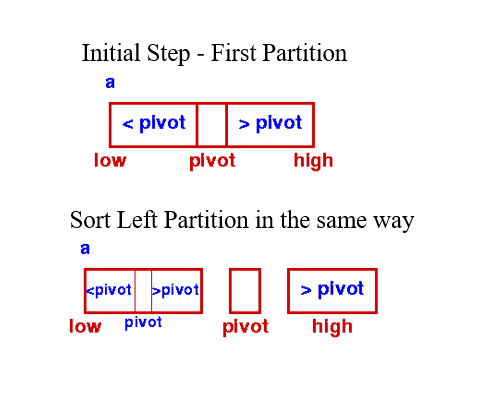
Quicksort – Partition phase
- Goals:
- Select pivot value
- Move everything less than pivot value to the left of it
- Move everything greater than pivot value to the right of it
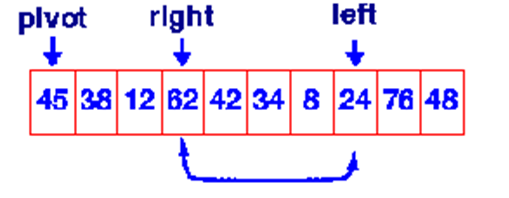
Algorithm: Quick Sort
Procedure QuickSort ( A, l, r )
if ( r > l ) then
j ¬ partition ( A, l, r );
QuickSort ( A, l, j – 1 );
QuickSort ( A, j + 1 , r );
end of if.
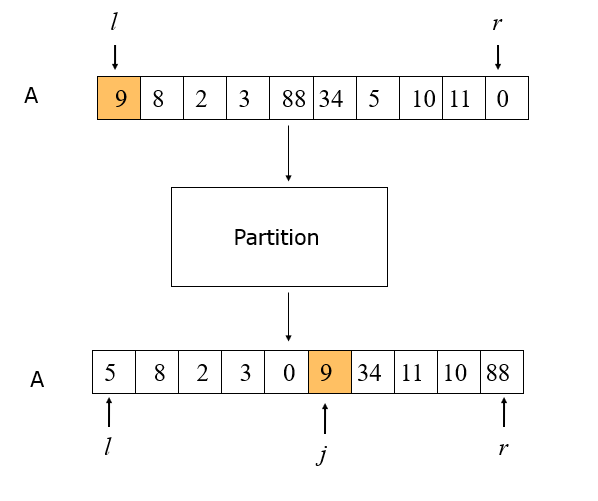
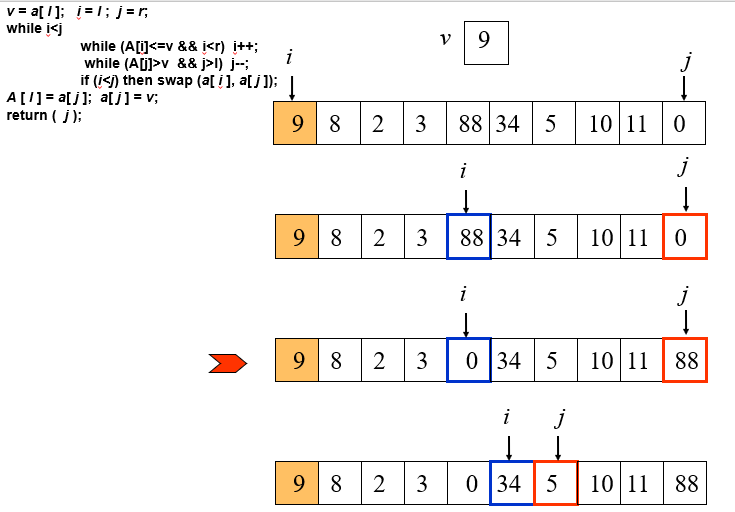
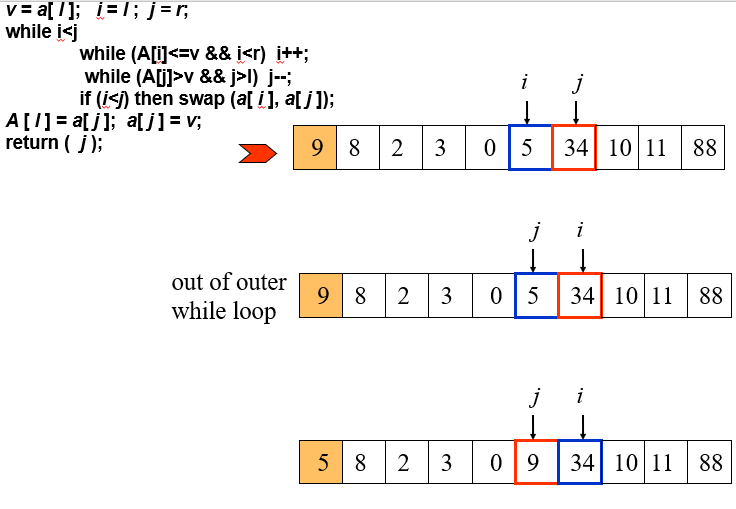
Function Partition (A, l, r )
v ¬ a[ l ]; i ¬ l ; j ¬ r;
while i<j
while (A[i]<=v && i<r) i++;
while (A[j]>v && j>l) j–;
if (i<j) then swap (a[ i ], a[ j ]);
A [ l ] = a[ j ]; a[ j ] ¬ v;
return ( j );
There are various algorithms for partition.
Above Algorithm does not need an extra array.
Only 3 variables v,i, and j are used.

Time Complexity: Best case/average case
- Recurrence Relation
T(n)=2T(n/2) + n
Using Master Theorem applying case 2:
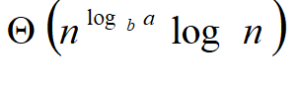
So time complexity is O(nlogn)
- Why is quick sort better than merge sort?
- Better memory consumption
The worst case is when the input is already sorted.


Randomized Quick Sort
- Randomize the input data before giving it to Quick Sort. OR
- In the partition phase, rather than choosing first value to be the pivot value, choose a RANDOM value to be pivot value.
- This makes Quick Sort run time independent of input ordering
- So Worst case won’t happen for SORTED inputs but may only happen by worseness of random number generator.
C++ code for quick sort using recursive function
#include <cstdlib>
#include <iostream>
#include<time.h>
#include<conio.h>
#define size 10
using namespace std;
void swap(int&a,int&b)
{
int tmp=a; a=b; b=tmp;
}
void quicksort(int a[],int left,int right)
{
int i=left,j=right,x=(left+right)/2,pivot=a[x];
while(1)
{
while(a[i]<pivot) i++;
if(i>x)break;
while(a[j]>pivot) j–;
if(j<x)break;
if(i<=j)
{
swap(a[i],a[j]);
i++;
j–;
}
}
if(j>left)
quicksort(a,left,j);
if(i<right)
quicksort(a,i,right);
}
int main()
{
srand(time(0));
int a[size],j=10;
for(int i=0;i<size;i++)
a[i]=rand()%100;
cout<<“Original Array: “;
for(int i=0;i<size;i++)
cout<<a[i]<<” “;
cout<<endl<<endl;
quicksort(a,0,size-1);
cout<<“Sorted Array: “;
for(int i=0;i<size;i++)
cout<<a[i]<<” “;
cout<<endl<<endl;
getch();
return EXIT_SUCCESS;
}
Related links
Single link list Stack AVL Trees Binary search Counting Sort
Doubly link list Queue Graphs Bubble Sort Radix sort
Circular link list Binary search tree Hashing Insertion Sort Bucket Sort
Josephus Problem Tree Traversal Heaps Quick Sort Merge Sort
At Cui tutorial, courses, past papers and final year projects
#tutorial #cui #pastpaper #courses

