Heaps
This lab teaches you the following topics:
- How to insert and delete data from heap
- How to find minimum value
Why Heaps?
Queues are a standard mechanism for ordering tasks on a first-come, first-served basis. In many situations, simple queues are inadequate, since first in/first out scheduling has to be overruled using some priority criteria like:
- In a sequence of processes, process P2 may need to be executed before process P1 for the proper functioning of a system, even though P1 was put on the queue of waiting processes before P2.
- Banks managing customer information often will remove or get the information about the customer with the minimum bank account
- In shared printer queue list of print jobs, must get next job with highest priority, and higher-priority jobs always print before lower-priority jobs.
In situations like these, a modified queue or priority queue, is needed in which elements are dequeued according to their priority and their current queue positions. The problem with a priority queue is in finding an efficient implementation which allows relatively fast enqueuing and dequeuing. Since elements may arrive randomly to the queue, there is no guarantee that the front elements will be the most likely to be dequeued and that the elements put at the end will be the last candidates for dequeuing. The situation is complicated because a wide spectrum of possible priority criteria can be used in different cases.
Consider an example of a printer; if the three jobs have been submitted to print, the jobs have sizes 100, 10, 1 page. The average waiting time for FIFO service, (100+110+111)/3 = 107 time units and average waiting time for shortest job first service, (1+11+112)/3 = 41 time units.
So a heap is an excellent way to implement a priority queue as binary heap is a complete or almost complete binary tree which satisfies the heap ordering property. The ordering can be one of two types: the min-heap property: the value of each node is greater than or equal to the value of its parent, with the minimum-value element at the root and max-heap each node is smaller than its parent node.
Heaps
Heap has the following properties:
- The value of each node is not less than the values stored in each of its children
- The tree is an almost complete binary
These two properties define a max heap and if ―less‖ in the first property is replaced with greater; then the definition specifies a min heap.
Heap is generally preferred for priority queue implementation by array list because it provide better performance as a method getHighestPriority() to access the element with highest priority can be implemented in O(1) time, method to insert() new element can be implemented in O(Logn) time and deleteHighestPriority() can also be implemented in O(Logn) time.
Applications of Priority Queue:
- CPU Scheduling
- Graph algorithms like Dijkstra’s shortest path algorithm, Prim’s Minimum Spanning Tree, etc
- All queue applications where priority is involved
A Binary Heap is a Binary Tree with following properties:
- It’s a complete tree (All levels are completely filled except possibly the last level and the last level has all keys as left as possible). This property of Binary Heap makes them suitable to be stored in an array.
- A Binary Heap is either Min Heap or Max Heap. In a Min Binary Heap, the key at root must be minimum among all keys present in Binary Heap. The same property must be recursively true for all nodes in Binary Max Binary Heap is similar to MinHeap.
Examples of Min-Heap

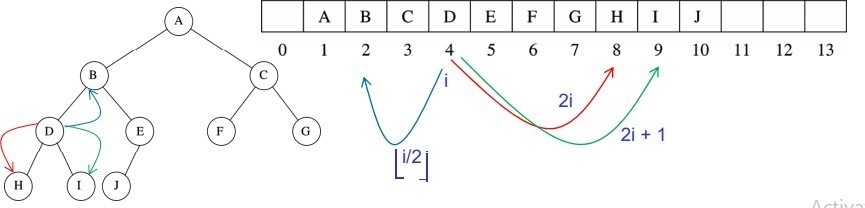
How is Binary Heap represented?
Given element at position i in the array:
- Left child (i) = at position 2i
- Right child(i) = at position 2i + 1
- Parent(i) = at position [i / 2 ]
Lab Activities:
Activity 1:
Write a program to insert and delete the data from a heap while maintaining its properties.
Solution:
// A C++ program to demonstrate common Binary Heap Operations
#include<iostream>
#include<climits>
using namespace std;
// Prototype of a utility function to swap two integers
void swap(int *x, int *y);
// A class for Min Heap
class MinHeap
{
int *harr; // pointer to array of elements in heap
int capacity; // maximum possible size of min heap
int heap_size; // Current number of elements in min heap
public:
// Constructor
MinHeap(int capacity);
// to heapify a subtree with the root at given index
void MinHeapify(int );
int parent(int i)
{
return (i-1)/2;
}
// to get index of left child of node at index i
int left(int i)
{
return (2*i + 1);
}
// to get index of right child of node at index i
int right(int i)
{
return (2*i + 2);
}
// to extract the root which is the minimum element
int extractMin();
// Decreases key value of key at index i to new_val
void decreaseKey(int i, int new_val);
// Returns the minimum key (key at root) from min heap
int getMin()
{
return harr[0];
}
// Deletes a key stored at index i
void deleteKey(int i);
// Inserts a new key ‘k’
void insertKey(int k);
};
// Constructor: Builds a heap from a given array a[] of given size
MinHeap::MinHeap(int cap)
{
heap_size = 0;
capacity = cap;
harr = new int[cap];
}
// Inserts a new key ‘k’
void MinHeap::insertKey(int k)
{
if (heap_size == capacity)
{
cout << “\nOverflow: Could not insertKey\n”;
return;
}
// First insert the new key at the end
heap_size++;
int i = heap_size – 1;
harr[i] = k;
// Fix the min heap property if it is violated
while (i != 0 && harr[parent(i)] > harr[i])
{
swap(&harr[i], &harr[parent(i)]);
i = parent(i);
}
}
// Decreases value of key at index ‘i’ to new_val. It is assumed that new_val is smaller than harr[i].
void MinHeap::decreaseKey(int i, int new_val)
{
harr[i] = new_val;
while (i != 0 && harr[parent(i)] > harr[i])
{
swap(&harr[i], &harr[parent(i)]); i = parent(i);
}
}
// Method to remove minimum element (or root) from min heap
int MinHeap::extractMin()
{
if (heap_size <= 0)
return INT_MAX;
if (heap_size == 1)
{
heap_size–;
return harr[0];
}
// Store the minimum value, and remove it from heap
int root = harr[0];
harr[0] = harr[heap_size-1];
heap_size–;
MinHeapify(0);
return root;
}
// This function deletes key at index i. It first reduced value to minusinfinite, then calls extractMin()
void MinHeap::deleteKey(int i)
{
decreaseKey(i, INT_MIN);
extractMin();
}
// A recursive method to heapify a subtree with the root at given index This method assumes that the subtrees are already heapified
void MinHeap::MinHeapify(int i)
{
int l = left(i);
int r = right(i);
int smallest = i;
if (l < heap_size && harr[l] < harr[i])
smallest = l;
if (r < heap_size && harr[r] < harr[smallest])
smallest = r;
if (smallest != i)
{
swap(&harr[i], &harr[smallest]);
MinHeapify(smallest);
}
}
// A utility function to swap two elements
void swap(int *x, int *y)
{
int temp = *x;
*x = *y;
*y = temp;
}
// Driver program to test above functions
int main()
{
MinHeap h(11);
h.insertKey(3);
h.insertKey(2);
h.deleteKey(1);
h.insertKey(15);
h.insertKey(5);
h.insertKey(4);
h.insertKey(45);
cout << h.extractMin() << ” “;
cout << h.getMin() << ” “;
h.decreaseKey(2, 1);
cout << h.getMin();
return 0;
}
Home Activities:
- Revise the heap definition of above class to implement a max- heap. The member function removemin should be replaced by a new function called removemax.
- Build the Huffman coding tree and determine the codes for the following set of letters and weights:
| Letter | A | B | C | D | E | F | G | H | I | J | K | L |
| Frequency | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 31 | 37 | 41 |
3.Implement a priority queue class based on the max-heap class implementation. The following methods should be supported for manipulating the priority queue:
-
-
- void enqueue(int ObjectID, int priority);
- int dequeue();
- void changeweight(int ObjectID, int newPriority);
-
Method enqueue inserts a new object into the priority queue with ID number ObjectID and priority priority. Method dequeue removes the object with highest priority from the priority queue and returns its object ID. Method changeweight changes the priority of the object with ID number ObjectID to be newPriority. The type for Elem should be a class that stores the object ID and the priority for that object. You will need a mechanism for finding the position of the desired object within the heap. Use an array, storing the object with ObjectID i in position i. (Be sure in your testing to keep the ObjectIDs within the array bounds.) You must also modify the heap implementation to store the object’s position in the auxiliary array so that updates to objects in the heap can be updated as well in the array.
4.You are required to design a computer program for a printer. Suppose there are N printing Jobs in a queue to be done, and each job has its own priority. The job with maximum priority (less number of pages) will get completed first than others. At each instant we are completing a job with maximum priority and at the same time we are also interested in inserting a new job in the queue with its own priority. Your maintained priority queue must fulfill the following conditions:
-
-
- getHighestPriority() should be implemented in O(1) time
- insert() should be implemented in O(Logn) time
- deleteHighestPriority() should also be implemented in O(Logn)
-
Related links
Single link list Stack AVL Trees Binary search Counting Sort
Doubly link list Queue Graphs Bubble Sort Radix sort
Circular link list Binary search tree Hashing Insertion Sort Bucket Sort
Josephus Problem Tree Traversal Heaps Quick Sort Merge Sort
At Cui tutorial, courses, past papers and final year projects
#tutorial #cui #pastpaper #courses

