How to create hash tables

• How to implement hash function
• How to insert, search and retrieve values from hash tables

 

 Introduction

Hashing is an improvement over Direct Access Table.

The idea is to use hash function that converts a given key to a smaller number and uses the small number as index in a table called hash table.

 

Example:

 

Suppose we want to design a system for storing employee records keyed using phone numbers. And we want following queries to be performed efficiently:

1. Insert a phone number and corresponding
2. Search a phone number and fetch the
3. Delete a phone number and related information.

We can think of using the following data structures to maintain information about different phone numbers.

1. Array of phone numbers and
2. Linked List of phone numbers and
3. Balanced binary search tree with phone numbers as keys
4. Direct Access

 

For arrays and linked lists, we need to search in a linear fashion, which can be costly in practice. If we use arrays and keep the data sorted, then a phone number can be searched in O(Logn) time using Binary Search, but insert and delete operations become costly as we have to maintain sorted order.

 

With balanced binary search tree, we get moderate search, insert and delete times. All of these operations can be guaranteed to be in O(Logn) time.

 

Another solution that one can think of is to use a direct access table where we make a big array and use phone numbers as index in the array. An entry in array is NIL if phone number is not present, else the array entry stores pointer to records corresponding to phone number. Time complexity wise this solution is the best among all, we can do all operations in O(1) time. For example to insert a phone number, we create a record with details of given phone number, use phone number as index and store the pointer to the created record in table. This solution has many practical limitations. First problem with this solution is extra space required is huge. For example if phone number is n digits, we need O(m * 10ⁿ) space for table where m is size of a pointer to record. Another problem is an integer in a programming language may not store n digits.

 

Due to above limitations Direct Access Table cannot always be used. Hashing is the solution that can be used in almost all such situations and performs extremely well compared to above data structures like Array, Linked List, Balanced BST in practice. With hashing we get O(1) search time on average (under reasonable assumptions) and O(n) in worst case.

 

Hash Function:

 

A function that converts a given big number to a small practical integer value.

The mapped integer value is used as an index in hash table.

In simple terms, a hash function maps a big number or string to a small integer that can be used as index in hash table.

For example, a person’s name, having a variable length, could be hashed to a single integer.

The values returned by a hash function are called hash values, hash codes, hash sums, checksums or simply hashes as shown in figure below:

 

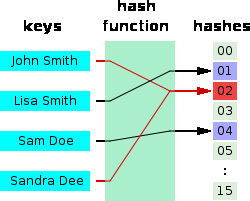
A good hash function should have following properties

 

• Efficiently computable

 

• Should uniformly distribute the keys (Each table position equally likely for each key)

 

 

Hash Table:

 

An array that stores pointers to records corresponding to a given phone number. An entry in hash table is NIL if no existing phone number has hash function value equal to the index for the entry.

 

Collision Handling:

 

Since a hash function gets us a small number for a big key, there is possibility that two keys result in same value. The situation where a newly inserted key maps to an already occupied slot in hash table is called collision and must be handled using some collision handling technique. Following are the ways to handle collisions:

• Chaining: The idea is to make each cell of hash table point to a linked list of records that have same hash function value. Chaining is simple, but requires additional memory outside the

 

• Open Addressing: In open addressing, all elements are stored in the hash table itself. Each table entry contains either a record or When searching for an element, we one by one examine table slots until the desired element is found or it is clear that the element is not in the table.

Lab Activities:

Activity 1:

Write a function to compute a simple hash function

 

Solution:

Activity 2:

Write a function to insert an item in a hash table

 

Solution:

 

Activity 3:

Write a function to search an item from hash table

 

Solution:

 

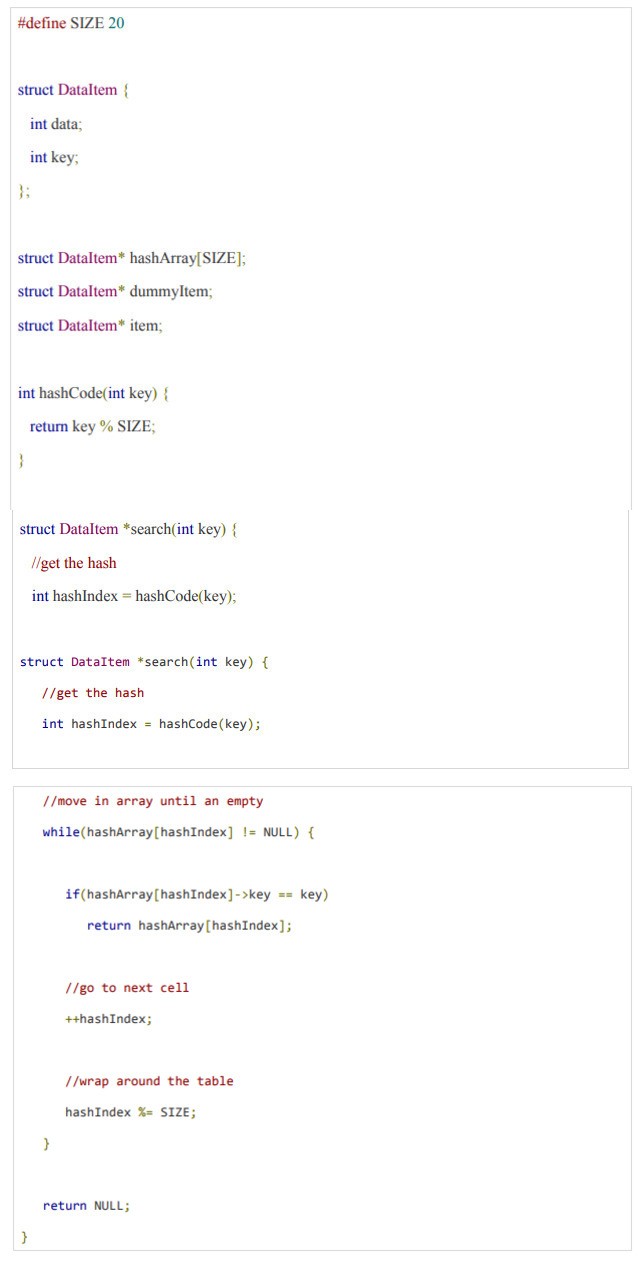
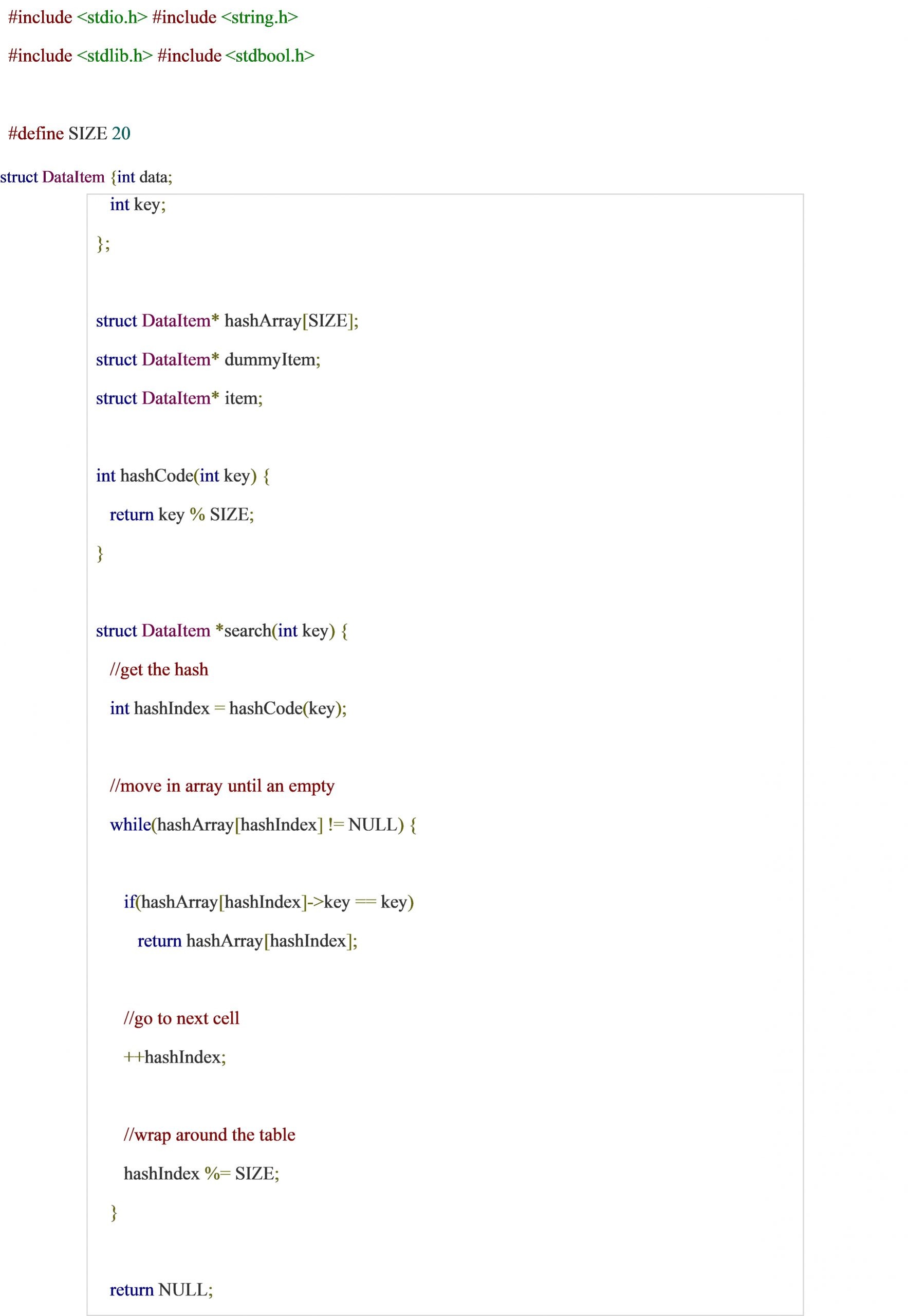
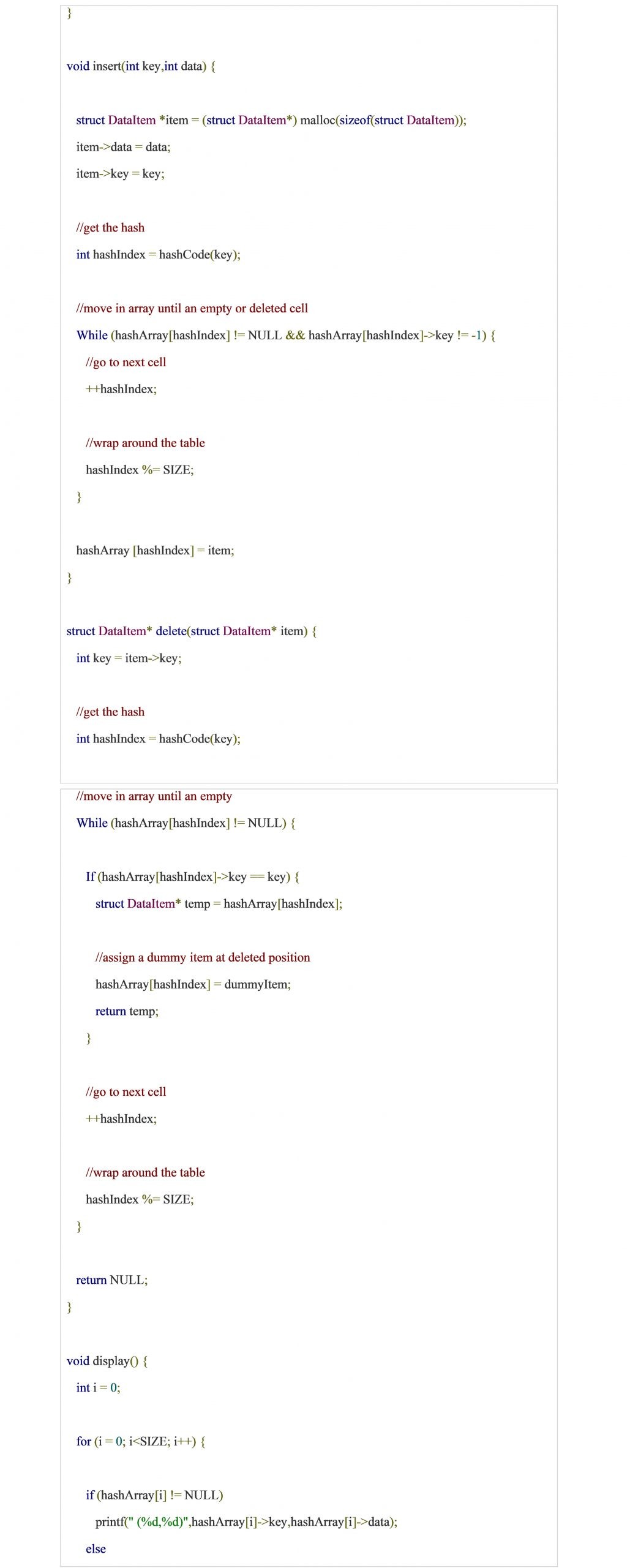
Activity 4:

Write a complete program to create a hash table using simple division hash function. Also perform searching and deletion in hash table.

 

Solution:

 

Home Activities:

• Consider ―key mod 7‖ as a hash function and a sequence of keys as 50, 700, 76, 85, 92, 73, 101. Create hash table for to store these keys using linear probing.
• Use mid square hash function to store the data of employees of a company. Employee ids are:

4176, 5678, 5469, 1245, 8907

              Apply folding method to store the above

• Consider the data with keys: 24, 42, 34, 62, 73. Store this data into a hash table of size 10 using quadratic probing to avoid collision.
• Store the keys 18, 26, 35, 9, 64, 47, 96, 36, and 70 in an empty hash table of size 13 using double Use h(key) = key % 13 as a first hash function while the second hash function is: h_p(key) = 1 + key % 12

Related links 

Single link list                 Stack              AVL Trees             Binary search          Counting Sort

Doubly link list               Queue              Graphs                  Bubble Sort               Radix sort

Circular link list              Binary search tree       Hashing         Insertion Sort         Bucket Sort

Josephus Problem          Tree Traversal              Heaps                Quick Sort              Merge Sort

 

At Cui tutorial, courses, past papers and final year projects

#tutorial #cui #pastpaper #courses