How to insert and delete data from binary trees

• How to traverse and search the binary trees

Introduction

Non-Linear Data Structure-Trees

A tree is a Non-Linear Data Structure which consists of set of nodes called vertices and set of edges which links vertices

A binary tree is made of nodes, where each node contains a “left” reference, a “right” reference, and a data element. The topmost node in the tree is called the root.

Every node (excluding a root) in a tree is connected by a directed edge from exactly one other node. This node is called a parent. On the other hand, each node can be connected to arbitrary number of nodes, called children. Nodes with no children are called leaves, or external nodes. Nodes which are not leaves are called internal nodes. Nodes with the same parent are called siblings.

Recursive definition:

A binary tree is a finite set of nodes that is either empty or consists of a root and maximum of two disjoint binary trees called the left subtree and the right subtree. The binary tree may also have only right or left subtree.

Advantages of trees

Trees are so useful and frequently used, because they have some very serious advantages:

• Trees reflect structural relationships in the data
• Trees are used to represent hierarchies
• Trees provide an efficient insertion and searching
• Trees are very flexible data, allowing to move subtrees around with minumum effort

Terminology:

• Root Node: The starting node of a tree is called Root node of that tree
• Terminal Nodes: The node which has no children is said to be terminal node or leaf .
• Non-Terminal Node: The nodes which have children is said to be Non-Terminal Nodes
• Degree: The degree of a node is number of sub trees of that node
• Depth: The length of largest path from root to terminals is said to be depth or height of the tree
• Siblings: The children of same parent are said to be siblings
• Ancestors: The ancestors of a node are all the nodes along the path from the root to the node

Binary Search Trees

We consider a particular kind of a binary tree called a Binary Search Tree (BST). The basic idea behind this data structure is to have such a storing repository that provides the efficient way of data sorting, searching and retrieving.

A BST is a binary tree where nodes are ordered in the following way:

• each node contains three parts (left subtree, right subtree and data part
• the data/keys in the left subtree are less then the data/key in its parent node, in short L < P;
• the keys in the right subtree are greater the key in its parent node, in short P < R;

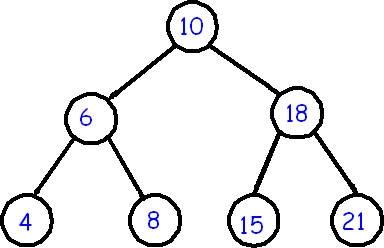
In the left tree all nodes in the left subtree of 10 have keys < 10 while all nodes in the right subtree > 10. Because both the left and right subtrees are again BST; the above definition is recursively applied to all internal nodes:

 

Lab Activities:

Activity 1:

Write a complete program to insert data into binary search tree.

Solution:

Complete binary search tree code 

Code

// Structure to store a Binary Search Tree node struct Node

{

int data;

Node *left, *right;

};

 

// Function to create a new binary tree node having given key

Node* newNode(int key)

{

Node* node = new Node;

node->data = key;

node->left = node->right = NULL;

 

return node;

}

 

// Recursive function to insert an key into BST using a reference parameter

void insert(Node* &root, int key)

{

// if the root is null, create a new node an return it

if (root == NULL)

{

root = newNode(key); return;

}

 

// if given key is less than the root node, recurse for left subtree

// else recurse for right subtree

if (key < root->data)

insert(root->left, key);

else          // key >= root->data

insert(root->right, key);

}

 

// main function

int main()

{

Node* root = NULL;

int keys[] = { 15, 10, 20, 8, 12, 16, 25 };

 

for (int i=0; i<7;i++)

insert(root, keys[i]);

 

return 0;

}

Activity 2:

Write functions for in-order, pre-order and post-order traversal of binary search trees.

Solution:

Pre-order Traversal

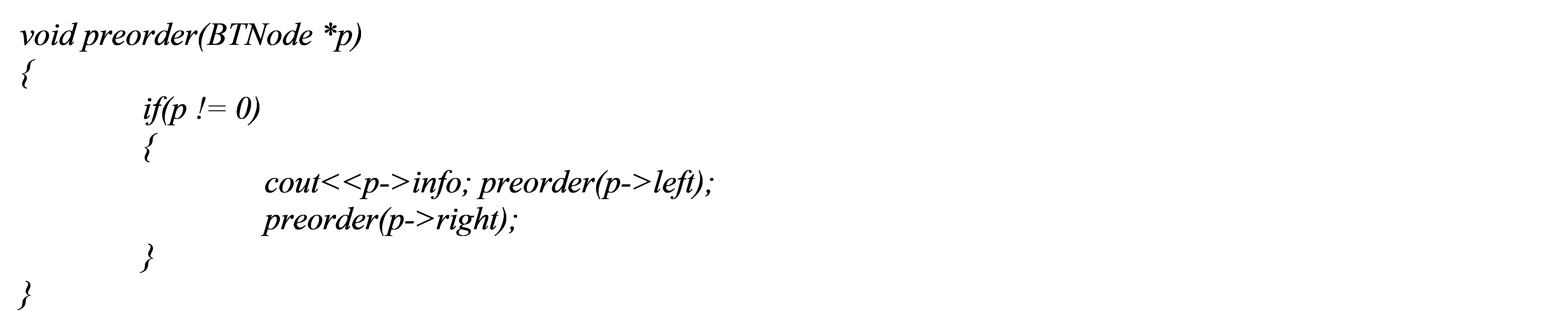
In-order Traversal

Post-order Traversal

 

Activity 3:

Write a function to search data in a binary tree.

Solution:

Activity 4:

Write a function to delete a node from binary tree.

Solution:

 

// Function to delete node from a BST

void deleteNode(Node*& root, int key)

{

// pointer to store parent node of current node

Node* parent = nullptr;

 

// start with root node

Node* curr = root;

 

// search key in BST and set its parent pointer

searchKey(curr, key, parent);

 

// return if key is not found in the tree

if (curr == nullptr)

return;

 

// Case 1: node to be deleted has no children i.e. it is a leaf node

if (curr->left == nullptr && curr->right == nullptr)

{

// if node to be deleted is not a root node, then set its

// parent left/right child to null

if (curr != root)

{

if (parent->left == curr)

parent->left = nullptr;

else

parent->right = nullptr;

}

// if tree has only root node, delete it and set root to null else

root = nullptr;

 

// deallocate the memory free(curr);      // or delete curr;

}

// Case 2: node to be deleted has two children

else if (curr->left && curr->right)

{

// find its in-order successor node

Node* successor = minimumKey(curr->right);

 

// store successor value

int val = successor->data;

 

// recursively delete the successor. Note that the successor

// will have at-most one child (right child) deleteNode(root, successor->data);

 

// Copy the value of successor to current node curr->data = val;

}

// Case 3: node to be deleted has only one child else

{

// find child node

Node* child = (curr->left)? curr->left: curr->right; 

// if node to be deleted is not a root node, then set its parent to its child

Activity 5:

Write a function to find minimum value in a subtree of binary search tree.

Solution:

Complete binary search tree code 

Home Activities:

Consider the BST in which you have stored the record of COMSATS’ students. The data

part of the BST is:

reg_num, name, address, phone_no and gpa

Write the following methods:

• Insert the record of new student (data is inserted by order of reg_num which is a unique number generated by rand() mehod).
• Search the record of student
• Display the record of student in ascending order
• Display record of student having highest GPA
• Calculate the average GPA of class
• Delete the record of specific student

1. What are the minimum and maximum number of elements in a heap of height h?
2. Where in a max-heap might the smallest element reside?
3. Show the max-heap that results from running buildHeap on the following values stored in an array:

10    5   12   3    2    1    8    7    9   4

4. (a) Show the heap that results from deleting the maximum value from the max-heap of Figure 20b.

(b) Show the heap that results from deleting the element with value 5 from the max-heap of Figure 5.20b.

5. Revise the heap definition of Figure 19 to implement a min-heap. The member function removemax should be replaced by a new function called removemin.
6. Build the Huffman coding tree and determine the codes for the following set of letters and weights:

Letter	A	B	C	D	E	F	G	H	I	J	K	L
Frequency	2	3	5	7	11	13	17	19	23	31	37	41

 

What is the expected length in bits of a message containing n characters for this frequency distribution?

7. What will the Huffman coding tree look like for a set of sixteen characters all with equal weight? What is the average code length for a letter in this case? How does this differ from the smallest possible fixed length code for sixteen characters?
8. A set of characters with varying weights is assigned Huffman codes. If one of the characters is assigned code 001, then,
   • Describe all codes that cannot have been
   • Describe all codes that must have been
9. Assume that a sample alphabet has the following weights:

Letter	Q	Z	F	M	T	S	O	E
Frequency	2	3	10	10	10	15	20	30

 

• For this alphabet, what is the worst-case number of bits required by the Huffman code for a string of n letters? What string(s) have the worst- case performance?
• For this alphabet, what is the best-case number of bits required by the Huffman code for a string of n letters? What string(s) have the best- case performance?
• What is the average number of bits required by a character using the Huffman code for this alphabet?

10. You must keep track of some Your options are:

• A linked-list maintained in sorted
• A linked-list of unsorted
• A binary search
• An array-based list maintained in sorted
• An array-based list of unsorted

For each of the following scenarios, which of these choices would be best? Explain your answer.

1. The records are guaranteed to arrive already sorted from lowest to high- est (i.e., whenever a record is inserted, its key value will always be greater than that of the last record inserted). A total of 1000 inserts will be interspersed with 1000
2. The records arrive with values having a uniform random distribution (so the BST is likely to be well balanced). 1,000,000 insertions are performed, followed by 10
3. The records arrive with values having a uniform random distribution (so the BST is likely to be well balanced). 1000 insertions are interspersed with 1000
4. The records arrive with values having a uniform random distribution (so the BST is likely to be well balanced). 1000 insertions are performed, followed by 1,000,000

• Write a C function that determines whether a given binary tree is a binary search
• Implement the BSTreeNumLeaves() which returns a count of the number of leaf nodes in the A leaf node is any node with empty left and right subtrees.
• Implement the BSTreeLevelOrder() function which prints the values in the BSTree in level-order on a single line separated by spaces (i.e. the same format as the other traverse-and-print functions). The following diagram aims to give an idea of how level-order traversal scans the nodes in a tree:

The output from this traversal would be 5 3 7 2 4 6 9 1 8.

Level-order traversal cannot be done recursively (at least not easily) and is typically implemented using a queue. The algorithm is roughly as follows:

4. write a function treeLeaves :: BinaryTree a -> [a]. This function should take a binary tree and return a list containing the leaves of that tree—that is, all the nodes with no subtrees beneath them.
5. The successor and predecessor methods take a node pointer as input and return the node pointer to the item that is the successor or predecessor to the input item. They should return NULL only if the input item is the max or min respectively. Each may return a pointer to a node of the same value if there are multiple copies of that value in the tree; either way, successive calls to each method should eventually move beyond the copies of that shared
6. Write the method to find the height the height of the tree.
7. Assume that a given BST stores integer values in its nodes. Write a recursive function that traverses a binary tree, and prints the value of every node who’s grandparent has a value that is a multiple of
8. Write a function that prints out the node values for a BST in sorted order from highest to
9. Write a recursive function named smallcount that, given the pointer to the root of a BST and a key K, returns the number of nodes having key values less than or equal to K. Function smallcountshould visit as few nodes in the BST as possible.
10. Write a recursive function named printRange that, given the pointer to the root to a BST, a low key value, and a high key value, prints in sorted order all records whose key values fall between the two given keys. Function printRange should visit as few nodes in the BST as

Related links 

Single link list                 Stack              AVL Trees             Binary search          Counting Sort

Doubly link list               Queue              Graphs                  Bubble Sort               Radix sort

Circular link list              Binary search tree       Hashing         Insertion Sort         Bucket Sort

Josephus Problem          Tree Traversal              Heaps                Quick Sort              Merge Sort

 

At Cui tutorial, courses, past papers and final year projects

#tutorial #cui #pastpaper #courses