Morphological Image Processing
- The word morphology commonly denotes a branch of biology that deals with the form and structure of animals and plants.
- We use the same word here in the context of mathematical morphology as a tool for extracting image components that are useful in the representation and description of region shape, such as boundaries, skeletons, and the convex hull.
- We are interested also in morphological techniques for pre- or post processing, such as morphological filtering, thinning, and pruning.
- In mathematics, the convex hull or convex envelope or convex closure of a set X of points in the Euclidean plane or in a Euclidean space (or, more generally, in an affine space over the reals) is the smallest convex set that contains X

Structuring Elements
- structuring elements (SEs): small sets or subimages used to probe an image under study for properties of interest.
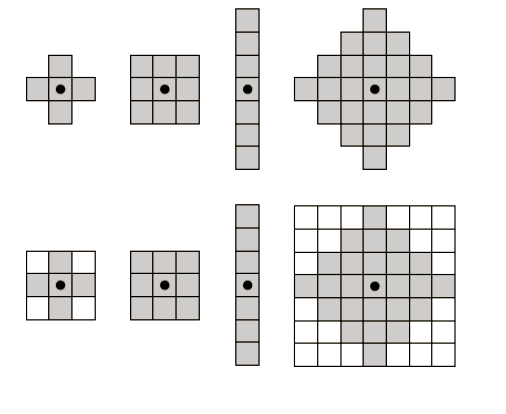
Example (How SE works on an image)
- Create a new set by running B over A so that the origin of B visits every element of A. At each location of the origin of B if B is completely contained in A, mark that location as a member of the new set (shown shaded); else mark it as not being a member of the new set (shown not shaded).
- Eroded image is the result
B is completely contained in A means that A and B are completely overlapping
Erosion and Dilation
- We begin the discussion of morphology by studying two operations
- Erosion
- Dilation
- These operations are fundamental to morphological processing.
- In fact, many of the morphological algorithms discussed in this chapter are based on these two primitive operations
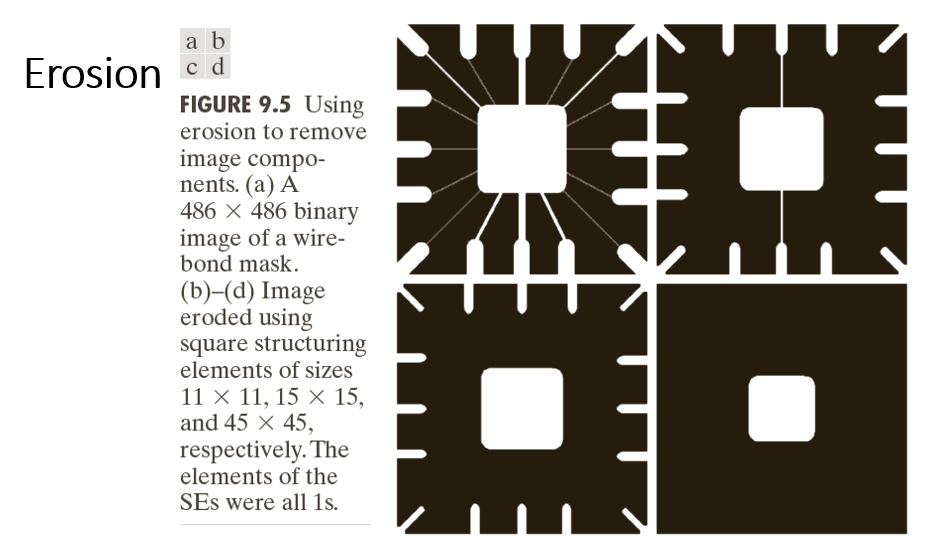
Erosion
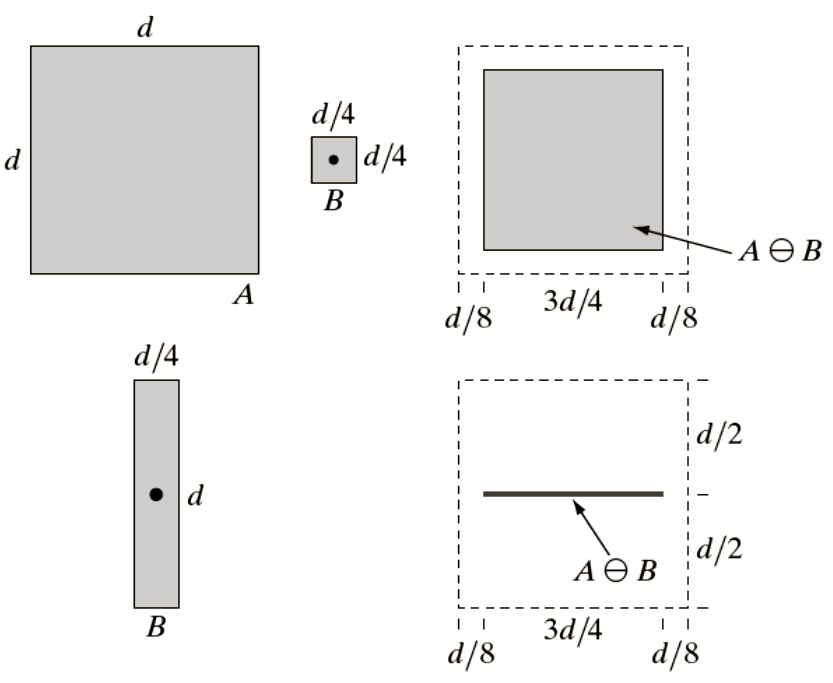
Dilation
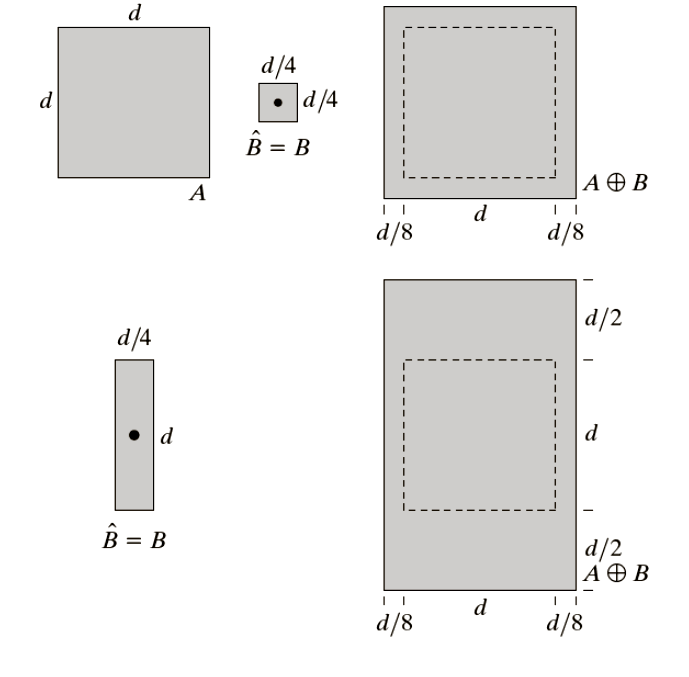
- A ⊕ B
- Reverse process of Erosion
- The element is marked in output when SE is overlapping partially or completely.
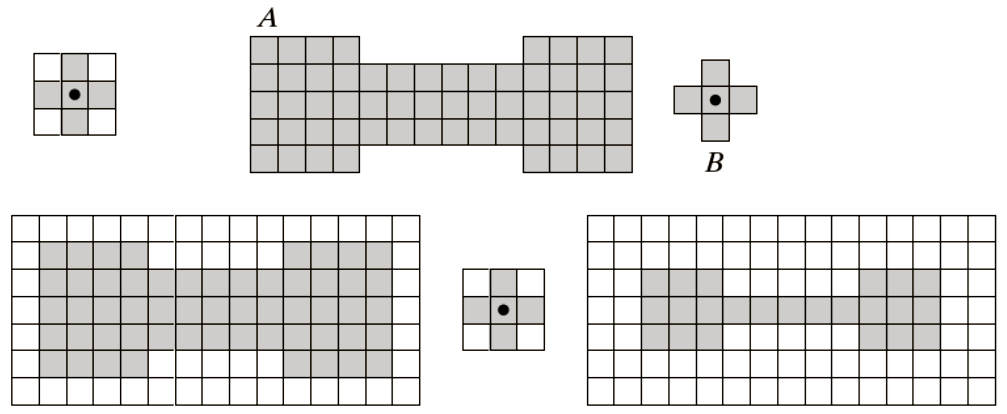
Example
- One of the simplest applications of dilation is for bridging gaps.
- Fig shows the same image with broken characters that we studied in
- The maximum length of the breaks is known to be two pixels.

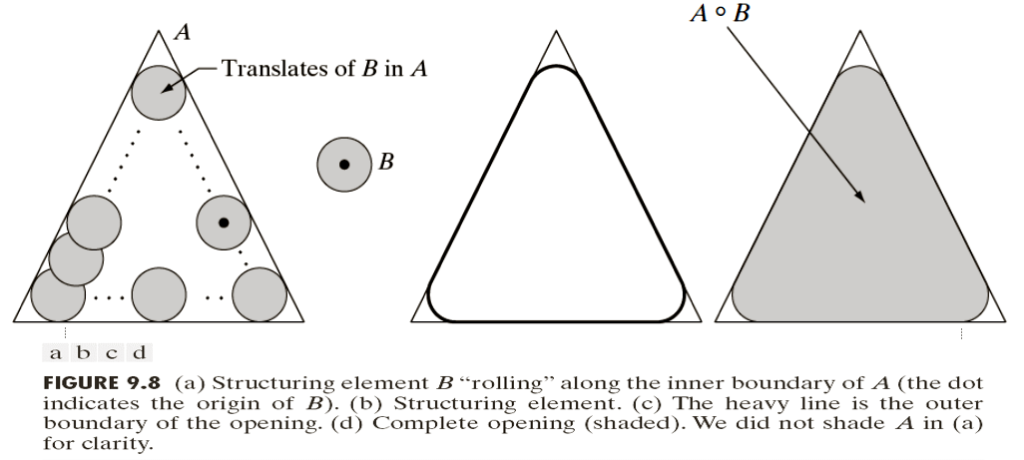
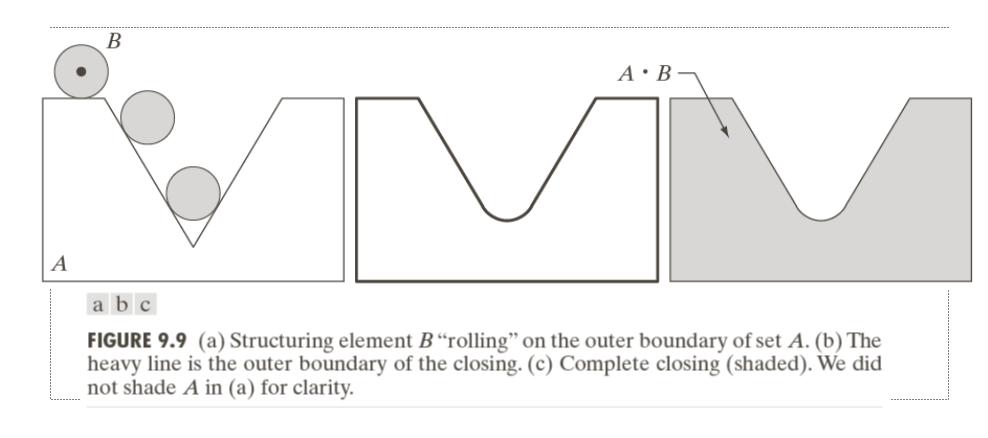
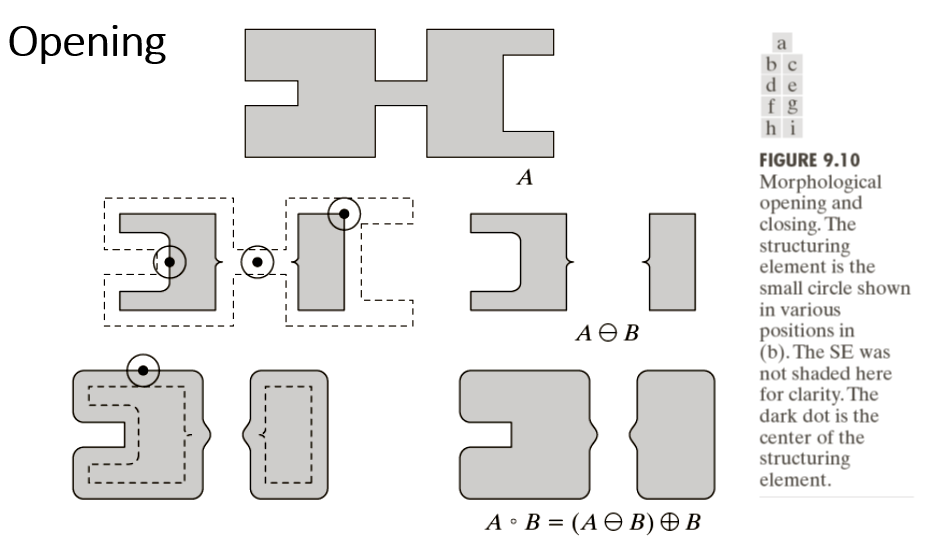
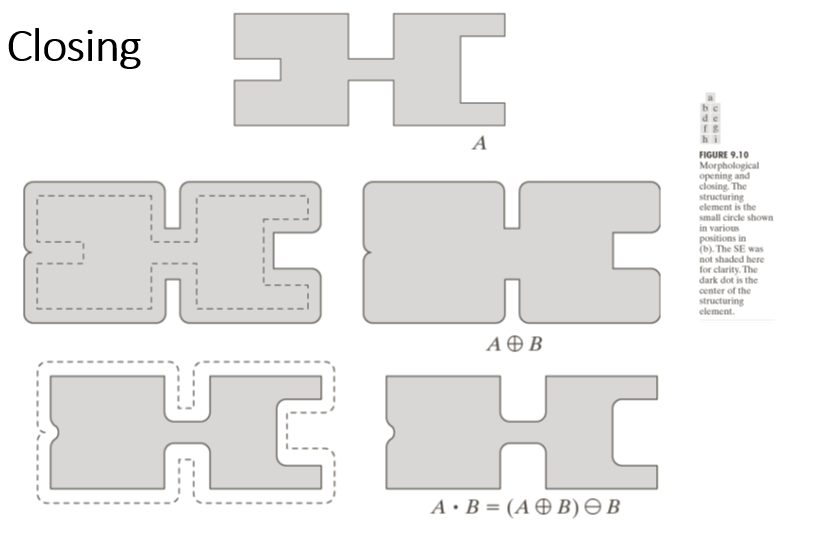
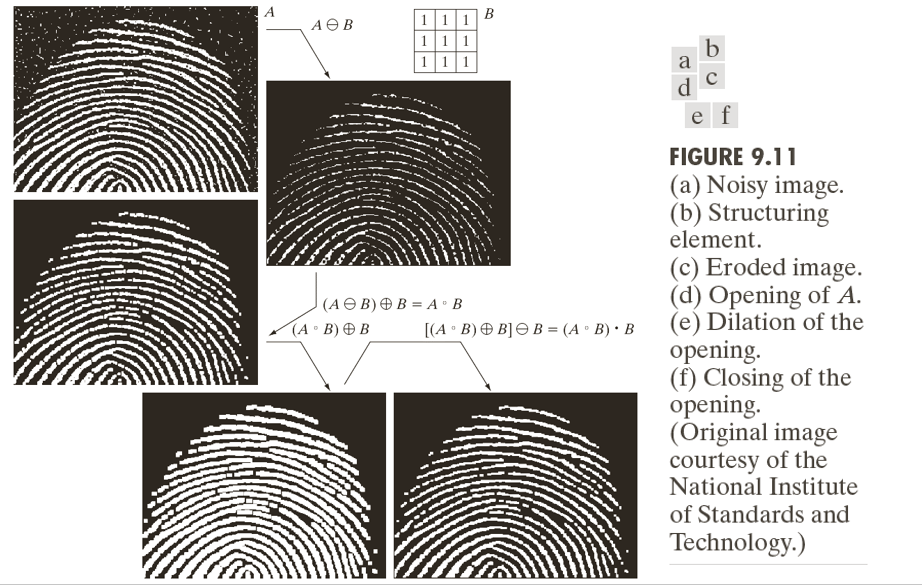
Opening and Closing
ØOpening generally smoothes the contour of an object, breaks narrow isthmuses, and eliminates thin protrusions.
ØA o B = ( A⊖B ) ⊕ B
Ø
ØClosing also tends to smooth sections of contours but, as opposed to opening, it generally fuses narrow breaks and long thin gulfs, eliminates small holes, and fills gaps in the contour.
ØA . B = ( A ⊕ B ) ⊖ B
Opening
Closing
Opening
The Hit-or-Miss Transformation
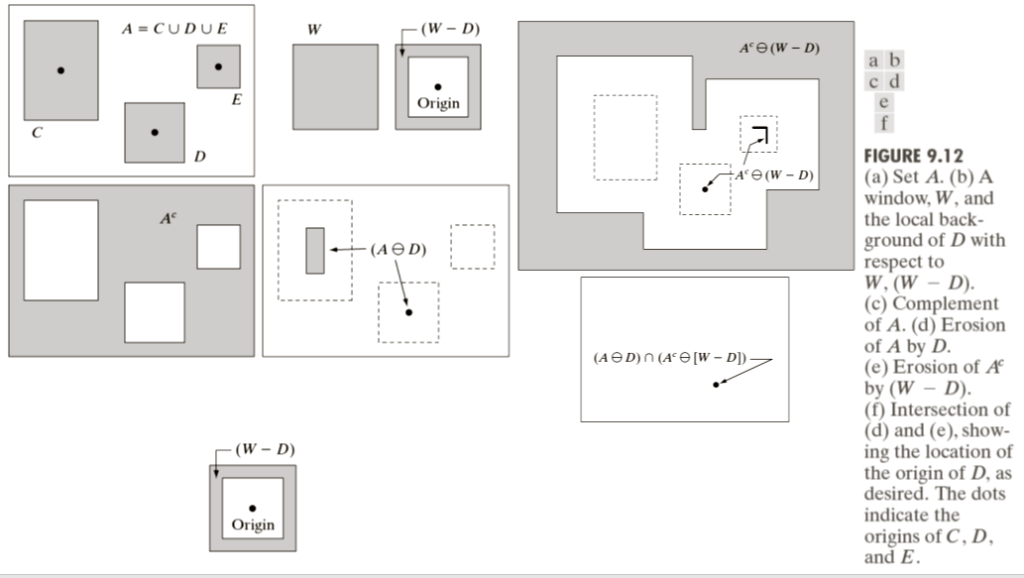
- The morphological hit-or-miss transform is a basic tool for shape detection
- This concept is introduced with the aid of Fig. 9.12, which shows a set consisting of three shapes (subsets), denoted C, D and E
- The shading in Figs. 9.12(a) through (c) indicates the original sets, whereas the shading in Figs. 9.12(d) and (e) indicates the result of morphological operations.
- The objective is to find the location of one of the shapes, say,D.

Hole Filling
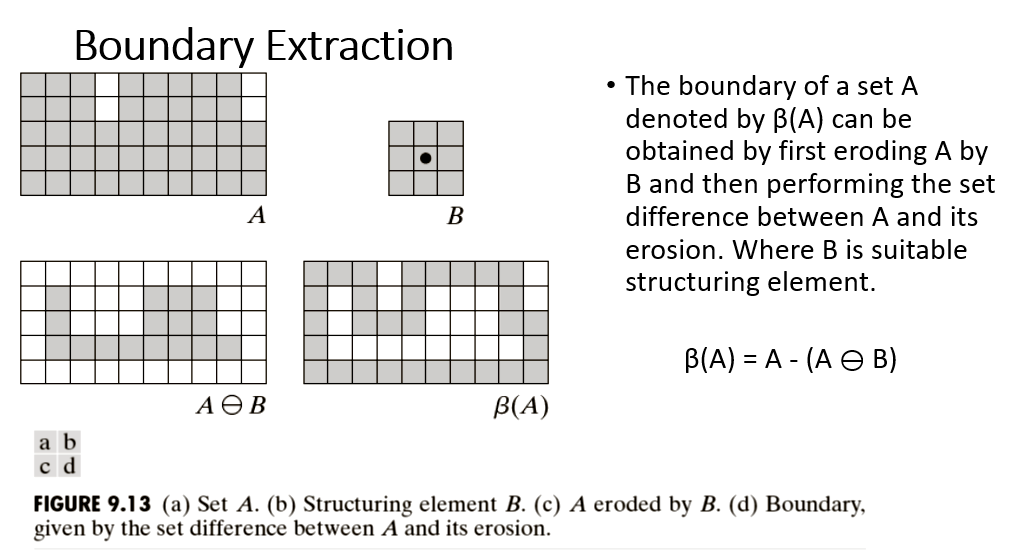
- A hole may be defined as a background region surrounded by a connected border of foreground pixels.
- To develop an algorithm based on dilation, complementation, and intersection for filling holes in an image.
- Let A denote a set whose elements are 8-connected boundaries, each boundary enclosing a background region (i.e., a hole).
- Given a point in each hole, the objective is to fill all the holes with 1s.
- We begin by forming an array, X0 , of 0s (the same size as the array containing A), except at the locations in corresponding to the given point in each hole, which we set to 1.
- Then, the following procedure fills all the holes with 1s
![]()
Related links

