ad

Basic Relationships Between Pixels

Advanced Image Processing

Basic Relationships Between Pixels

Neighborhood
Adjacency

Paths
Connectivity
Regions

Boundaries

Neighbors of a pixel – N4(p)

Any pixel p(x, y) has two vertical and two horizontal neighbors, given by

(x+1, y),

(x-1, y),

(x, y+1),

(x, y-1)

This set of pixels are called the 4-neighbors of P, and is denoted by N4(P).

	x , y+1
x-1 , y	x,y	x+1 , y
	x , y-1

Neighbors of a pixel – ND(p)

Any pixel p(x, y) has four diagonal neighbors, given by

(x+1, y+1), (x+1, y-1), (x-1, y+1), (x-1 ,y-1)

This set is denoted by ND(p).

x-1 , y+1		x+1, y+1
	x,y
x-1, y-1		x+1,y-1

Neighbors of a pixel – N8(p)

ND(p) and N4(p) are together known as 8-Neighbors and are denoted by N8(p)
ND(p) U N4(p) = N8(p)

What about when p(x,y) is a border pixel of the image ?

x-1,y+1	x,y+1	x+1,y+1
x-1,y	x,y	x+1,y
x-1,y-1	x,y-1	x+1, y-1

Adjacency

Let V be the set of intensity values used to define adjacency
For binary images à V = {1}

A particular grayscale image à V = {1,3,5,…,251,253,255}
4-adjacency: Two pixels p and q with values from V are 4-adjacent if q is in the set N4(p).
8-adjacency: Two pixels p and q with values from V are 8-adjacent if q is in the set N8(p).

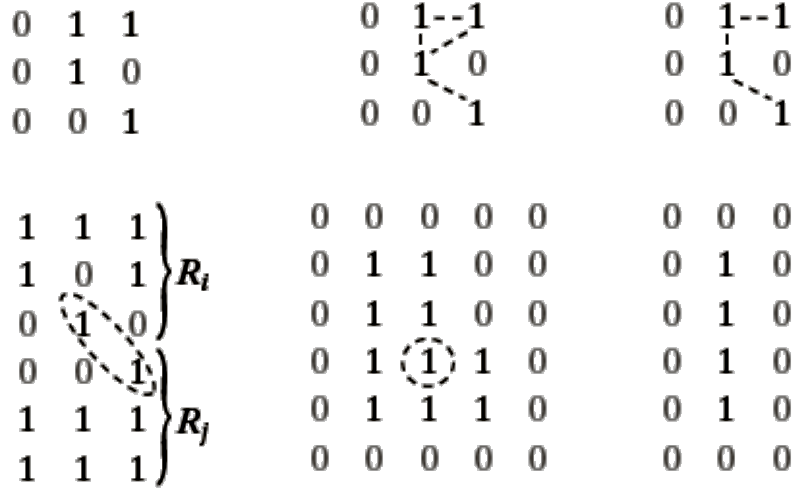
m-adjacency: Two pixels p and q with values from V are m-adjacent if,

q is in N4(p)

OR

q is in ND(p) AND N4(p)∩N4(q) has no pixels whose values are from V

Path

set of pixels lying in some adjacency definition
4-adjacency à 4-path
8-adjacency à 8-path

m-adjacency à m-path
path length ?
Number of pixels involved

Connectivity

Let Sà subset of pixels in an image
Two pixels p and q are said to be connected in S if there exist a path between them consisting entirely of pixels in S.
For any pixel p in S the set of pixels that are connected to it in S is called connected component of S.

If S has only one connected component, then it is called connected set.

Region

A connected set is also called a Region.
Two regions (let Ri and Rj) are said to be adjacent if their union forms a connected set. Adjacent Regions or joint regions

Regions that are not adjacent are said to be disjoint regions.
4- and 8-adjacency is considered when referring to regions (author)
Discussing a particular region, type of adjacency must be specified.

Fig2.25d the two regions are adjacent only if 8-adjacency is considered

Foreground and Background

Suppose an image contain K disjoint regions Rk , k=1,2,3,…K, none of which touches the image border
Let Ru denote the union of all the K regions.

Let (Ru)c denote its compliment.
We call all the points in Ru the foreground and all the points in (Ru)c the background

Boundary

The boundary (border or contour) of a region R is the set of points that are adjacent to the points in the complement of R.

Set of pixels in the region that have at least one background neighbor.
The boundary of the region R is the set of pixels in the region that have one or more neighbors that are not in R.
Inner Border: Border of Foreground

Outer Border: Border of Background
If R happens to be entire Image?
There is a difference between boundary and edge in Digital Image Paradigm. The author refers this discussion to chapter 10.

Distance Measures

Euclidean Distance: De(p, q) = [(x-s)2 + (y-t)2]1/2

City Block Distance: D4(p, q) = |x-s| + |y-t|

Chess Board Distance: D8(p, q) = max(|x-s|, |y-t|)

Sample Problem from exercise

Histogram Representation

Histograms plots how many times (frequency) each intensity value in image occurs
Image below (left) has 256 distinct gray levels (8 bits)

Histogram (right) shows frequency (how many times) each gray level occurs

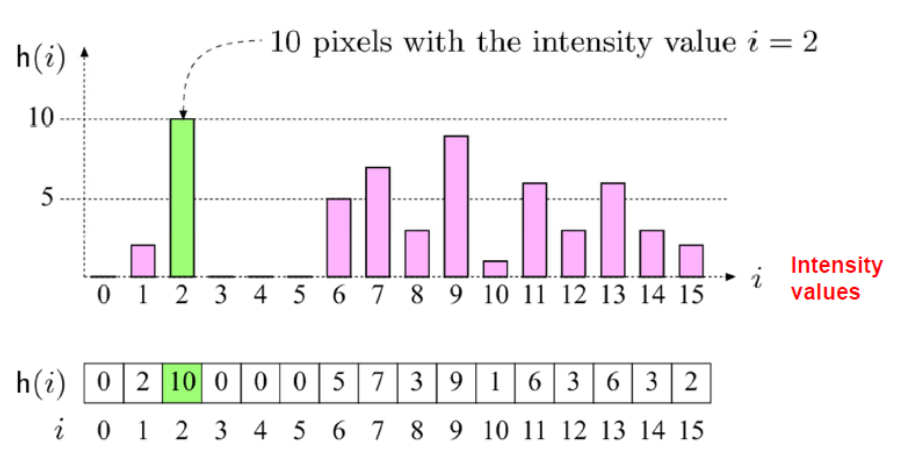
E.g. K = 16, 10 pixels have intensity value = 2
Only statistical information
No indication of location of pixels

Rough guess about the histogram of these images ?

Histogram Representation

Different images can have same histogram
3 images below have same histogram

Half of pixels are gray, half are white
Same histogram = Same statistics
Distribution of intensities could be different

Histogram Representation

Many cameras display real time histograms of scene
Helps taking pictures according to your requirement

Also easier to detect types of processing applied to image

?

Can we reconstruct image from histogram ?

Histogram

Histograms help detect image acquisition issues
Histogram representation of an image can be useful in following characteristics of an image.

Exposure: amount of light per unit area reaching the image sensor
Brightness: average intensity of all pixels in image
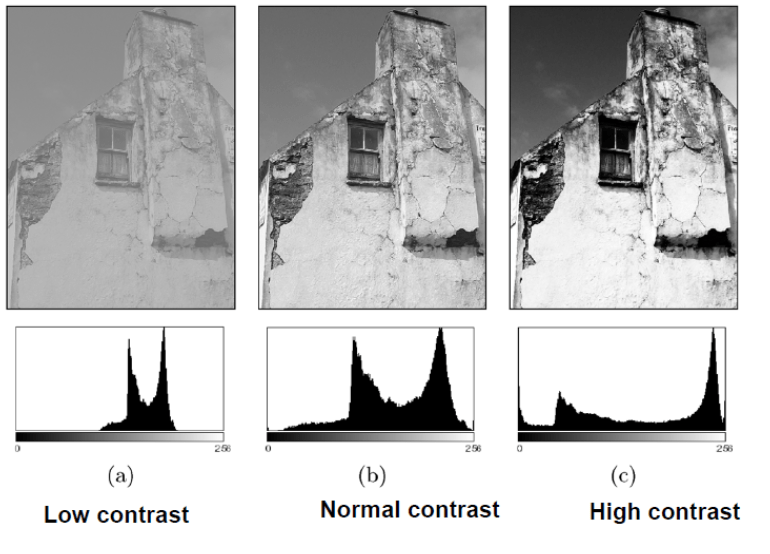
Contrast: difference of foreground and background (objects distinction)

Dynamic Range: Number of distinct pixels in image
Artifacts: Image alteration after it is being captured

Histogram Representation

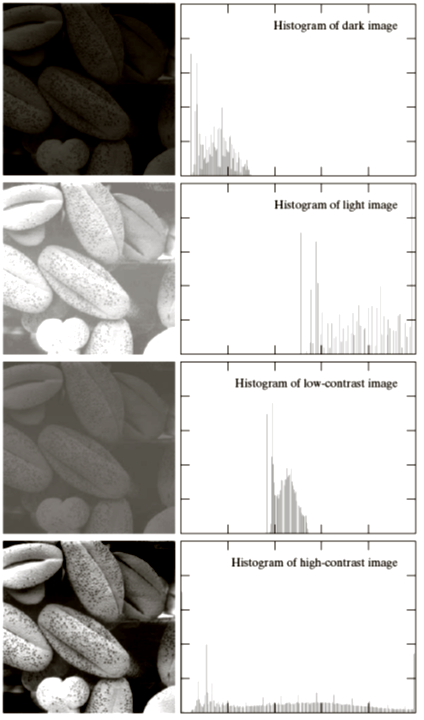
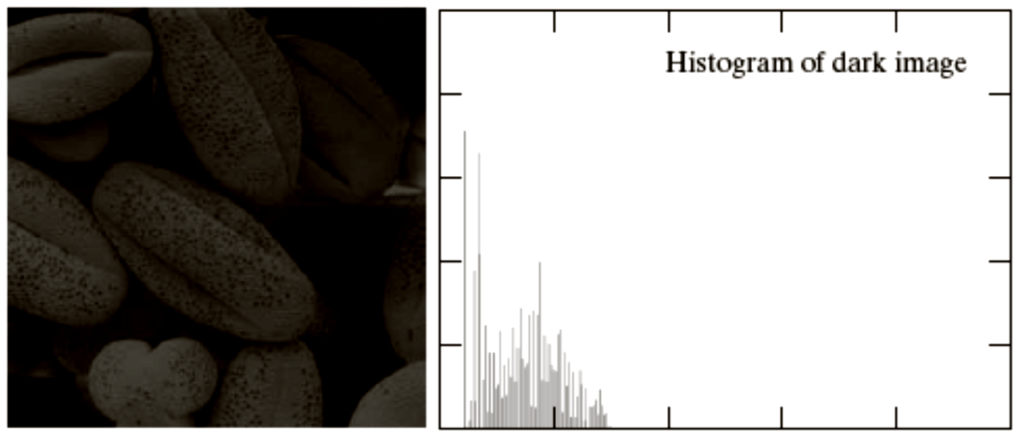
Four basic image types: dark, light, low contrast, high contrast and their corresponding histograms.

Histogram Representation

Histogram Representation

Histogram Representation

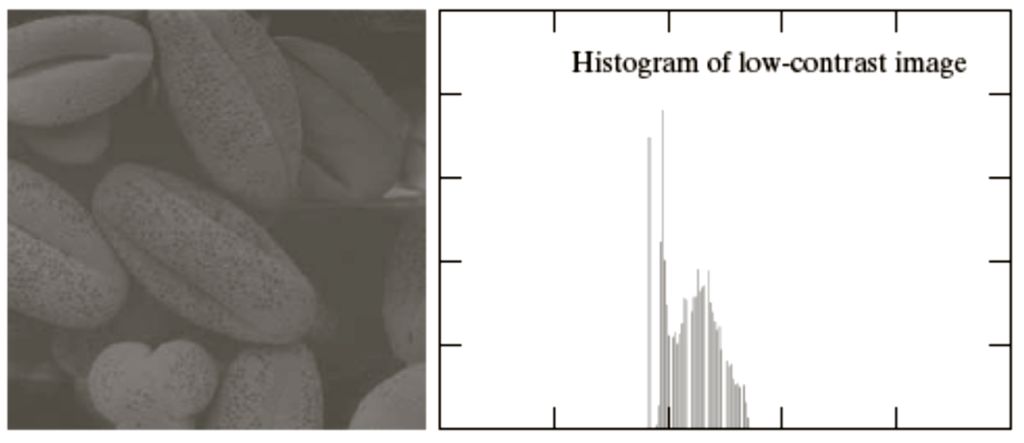
Histogram Representation

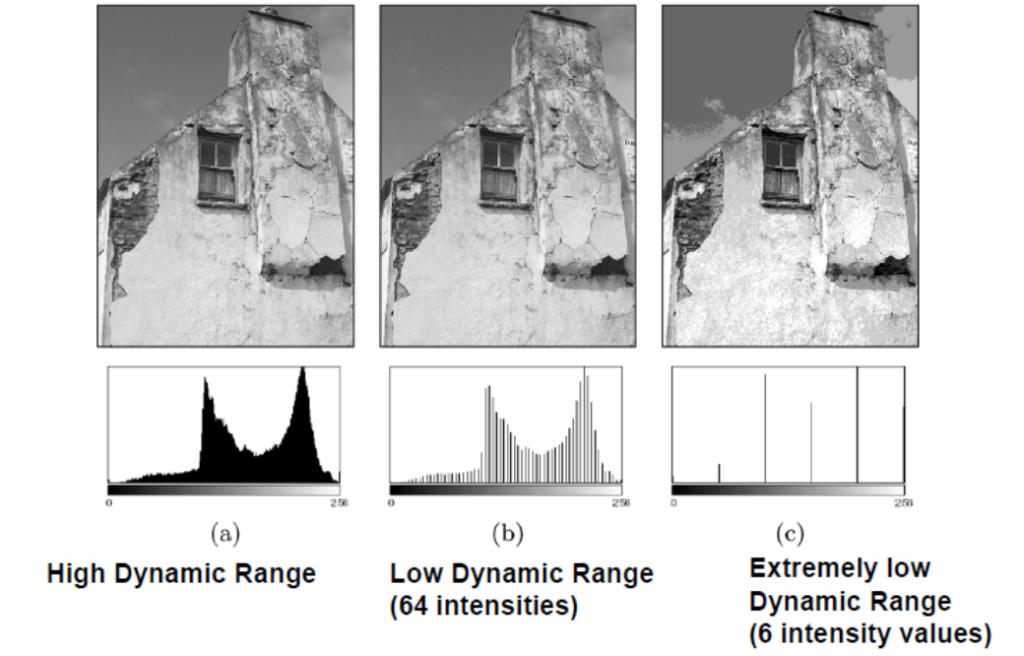
Contrast

Good Contrast?
Widely spread intensity values
Large difference between min and max intensity values

Related links

Basic Relationships Between Pixels

Search within CuiTutorial