First set of a given grammar using Array Compiler Construction
Syntax analysis is the second phase of a compiler.The lexical analyzer works closely with the syntax analyzer. It reads character streams from the source code, checks for legal tokens, and passes the data to the syntax analyzer for further processing.
Activity Outcomes:
- How to find the tokens/variables that are the starting symbols of a grammar
Instructor Note:
Students should know how to write grammar rules in C#
Introduction
Each time a predictive parser makes a decision, it needs to determine which production rule to apply to the leftmost non-terminal in an intermediate form, based on the next terminal (i.e. the lookahead symbol).
Take the minimalistic grammar
- S -> aAb
- A -> a | <epsilon>
and let us first parse the statement ‘aab’, so that the parser starts from looking at the (intermediate form, input) pair (‘S’,’aab’).
There is no real choice here (since ‘S’ expands in only one way), but we can still see that this is the production to choose because FIRST(S) = {a}, and arrive at the pair (‘aAb’, ‘aab’). If we started from (‘S’, ‘z’), we’d already know that there’s a syntax error, because no expansion of S begins with ‘z’ – that’s how come FIRST(S) doesn’t have a ‘z’ in it.
Moving along, (‘aAb’, ‘aab’) doesn’t begin with a non-terminal to decide a production for, so we just verify that ‘a’ matches ‘a’, which leaves us with (‘Ab’,’ab’). The nonterminal ‘A’ does have multiple ways to expand – it can either become an ‘a’, or vanish. Since FIRST(A) = {a} as well, the former choice is the right one, so we choose that, and get (‘ab’, ‘ab’). Having run out of nonterminals, the rest is just to verify that ‘a’ is in the right place to leave (‘b’,’b’), and ‘b’ matches as well, so in the end, the statement is accepted by the grammar.
This is the significance of the FIRST sets: they tell you when a nonterminal can produce the lookahead symbol as the beginning of a statement, so that it can be matched away and reduce the input. These derivations were direct, but if the grammar were
- S -> aDb
- D -> E
- E -> ‘a’ | <epsilon>
you would find ‘a’ in FIRST(S), FIRST(D), and FIRST(E) to drive essentially the same choices, just using one additional step of derivation.
First sets are the set of all what can begin a production rule. For example a number must begin
with a digit, a identifier must begin with a letter,…
Lab Activities:
Activity 1:
Write a program that takes at least six grammar rules. Based on these rules, find the first sets of these non-terminals.
Solution:
C Program To Find First of a Given Grammar using Array
#include<stdio.h>
#include<ctype.h>
void Find_First(char[], char);
void Array_Manipulation(char[], char);
int limit;
char production[25][25];
int main()
{
char option; char ch;
char array[25]; int count;
printf(“\nEnter Total Number of Productions:\t”);
scanf(“%d”, &limit);
for(count = 0; count < limit; count++)
{
printf(“\nValue of Production Number [%d]:\t”, count + 1);
scanf(“%s”, production[count]);
}
do
{
printf(“\nEnter a Value to Find First:\t”);
scanf(” %c”, &ch);
Find_First(array, ch);
printf(“\nFirst Value of %c:\t{ “, ch);
for(count = 0; array[count] != ‘\0’; count++)
{
printf(” %c “, array[count]);
}
printf(“}\n”);
printf(“To Continue, Press Y:\t”);
scanf(” %c”, &option);
}while(option == ‘y’ || option == ‘Y’);
return 0;
}
void Find_First(char* array, char ch)
{
int count, j, k;
char temporary_result[20];
int x;
temporary_result[0] = ‘\0’;
array[0] = ‘\0’;
if(!(isupper(ch)))
{
Array_Manipulation(array, ch);
return ;
}
for(count = 0; count < limit; count++)
{
if(production[count][0] == ch)
{
if(production[count][2] == ‘$’)
{
}
else
{
Array_Manipulation(array, ‘$’);
j = 2;
while(production[count][j] != ‘\0’)
{
x = 0;
Find_First(temporary_result, production[count][j]);
for(k = 0; temporary_result[k] != ‘\0’; k++)
{
Array_Manipulation(array,temporary_result[k]);
}
for(k = 0; temporary_result[k] != ‘\0’; k++)
{
if(temporary_result[k] == ‘$’)
{
x = 1;
break;
}
}
if(!x)
{
break;
} j++;
}
}
}
}
return;
}
void Array_Manipulation(char array[], char value)
{
int temp;
for(temp = 0; array[temp] != ‘\0’; temp++)
{
if(array[temp] == value)
{
return;
}
}
array[temp] = value; array[temp + 1] = ‘\0’;
}
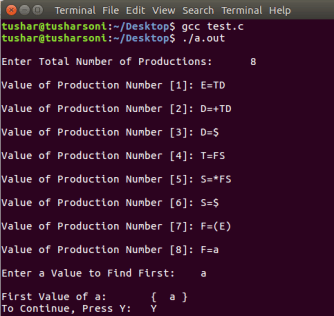
Output:
Home Activities:
Activity 1:
Write a code for any given grammar that satisfy the criterion of JAVA language constructs.
Assignment: Students must submit their home task before next lab.
Related Links
- Introduction to C#
- Lexical Analyzer Recognition of operators/variables
- Recognition of keywords/constants
- Lexical Analyzer Input Buffering scheme
- Symbol Table in Compiler Construction
- First set of a given grammar using Array
- Follow set of a given grammar using Array
- Bottom-up Parser-I DFA Implementation
- Bottom-up Parser-II Stack parser using SLR
- Semantic Analyzer
#Compiler Construction complete course # Compiler Construction past paper # Compiler Construction project #Computer Science all courses #University Past Paper #Programming language #Introduction to C# #Lexical Analyzer Recognition of operators/variables #Recognition of keywords/constants #Lexical Analyzer Input Buffering scheme #Symbol Table in Compiler Construction #First set of a given grammar using Array #Follow set of a given grammar using Array #Bottom-up Parser-I DFA Implementation #Bottom-up Parser-II Stack parser using SLR #Semantic Analyzer

