• Algorithm
• Named after a Muslim mathematician, Al-Khawarzmi

  (عَبْدَالله مُحَمَّد بِن مُوسَى اَلْخْوَارِزْمِي)

What is an Algorithms  ?

• Algorithm is a well defined computational procedure that takes some value (s) as input, and produces some value (s) as output.

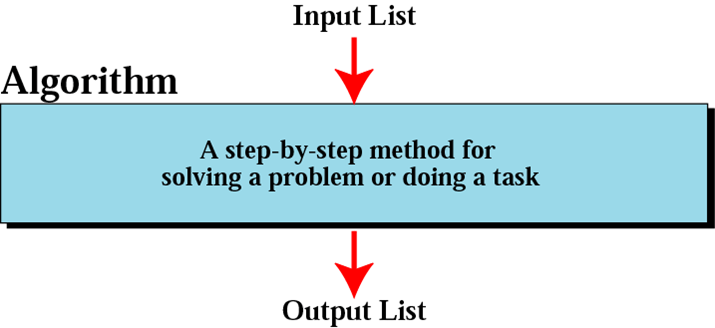
Algorithm Concepts

What is Data Structure?

A data structure is a systematic way of organizing and accessing data. Some basic data structure as follows.

• Array
• Link List
• Stacks
• Queues
• Trees

What is Program?

Program is an implementation of an algorithm in some programming language.

Data structure + Algorithm = Program

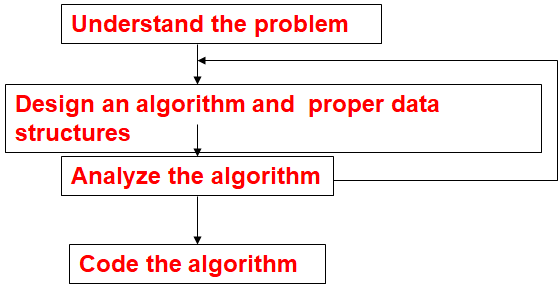
Design & Analysis of Algorithms

1.The “design” pertains to

1. i. The description of algorithm at an abstract level by means   of a pseudo language, and
2. Proof of correctness that is, the algorithm solves the given   problem in all cases.
3. The “analysis” deals with performance evaluation (complexity analysis).

Problem, Solution and Tools

1. A computer does not solve problems; it’s just a tool that I can use to implement my plan for solving the problem.
2. A computer program is a set of instructions for a computer. These instructions describe the steps that the computer must follow to   implement a plan.
3. An algorithm is a plan for solving a problem.
4. A person must design an algorithm.
5. A person must translate an algorithm into a computer program.

Algorithm Development Process

Good Algorithms?

• Run in less time
• Consume less memory

But computational resources (time complexity) is usually more important

Measuring Efficiency

• The efficiency of an algorithm is a measure of the amount of resources consumed in solving a problem of size n.
• The resource we are most interested in is time
• We can use the same techniques we will present to analyze the consumption of other resources, such as memory space.
• It would seem that the most obvious way to measure the efficiency of an algorithm is to run it and measure how much processor time is needed
• But is it correct???

Factors

• Hardware
• Operating System
• Compiler
• Size of input
• Nature of Input
• Algorithm

Which should be improved?

Running Time of an Algorithm

• Depends upon
• Input Size
• Nature of Input
• Generally time grows with size of input, so running time of an algorithm is usually measured as function of input size.
• Running time is measured in terms of number of steps/primitive operations performed
• Independent from machine, OS

Finding running time of an Algorithm / Analyzing an Algorithm

• Running time is measured by number of steps/primitive operations performed
• Steps means elementary operation like
• ,+, *,<, =, A[i] etc
• We will measure number of steps taken in term of size of input

Simple Example (1)

// Input: int A[N], array of N integers

// Output: Sum of all numbers in array A

int Sum(int A[], int N)

{

int s=0;

for (int i=0; i< N; i++)

s = s + A[i];

return s;

}

How should we analyse this?

Simple Example (2)

1,2,8: Once

3,4,5,6,7: Once per each iteration

of for loop, N iteration

Total: 5N + 3

The complexity function of the

algorithm is : f(N) = 5N +3

Simple Example (3)
Growth of 5n+3

Estimated running time for different values of N:

N = 10  => 53 steps

N = 100  => 503 steps

N = 1,000  => 5003 steps

N = 1,000,000  => 5,000,003 steps

As N grows, the number of steps grow in linear proportion to N for this function “Sum”

What Dominates in Previous Example?

What about the +3 and 5 in 5N+3?

• As N gets large, the +3 becomes insignificant
• 5 is inaccurate, as different operations require varying amounts of time and also does not have any significant importance

What is fundamental is that the time is linear in N.
Asymptotic Complexity: As N gets large, concentrate on the
highest order term:

• Drop lower order terms such as +3
• Drop the constant coefficient of the highest order term i.e. N

Asymptotic Complexity

• The 5N+3 time bound is said to “grow asymptotically” like N
• This gives us an approximation of the complexity of the algorithm
• Ignores lots of (machine dependent) details, concentrate on the bigger picture

Comparing Functions: Asymptotic Notation

• Big Oh Notation: Upper bound
• Omega Notation: Lower bound
• Theta Notation: Tighter bound

Big Oh Notation

If f(N) and g(N) are two complexity functions, we say

f(N)  = O(g(N))

(read “f(N) is order g(N)”, or “f(N) is big-O of g(N)”)

if there are constants c and N0 such that for N > N0,

f(N) ≤ c * g(N)

for all sufficiently large N.

• T(N) = 1000 N
• F(N) = N^2 is T(N)=O(F(N))?
• 1000N > N^2 for small values of N

Let N0 = 1000, c=1

Or N0 = 10, c=1000

1000N = O( N^2) at N= N0 = 1000

1000*1000 <= 1(1000)^2

• Compare the relative growth!
• T(N)= O(F(N)) or 1000N = O (N^2)

Example (1)

• Consider

f(n)=2n2+3

and g(n)=n2

Is f(n)=O(g(n))? i.e. Is 2n2+3 = O(n2)?

Proof:

2n2+3 ≤ c *  n2

Assume N0 =1 and c=1?

Assume N0 =1 and c=2?

Assume N0 =1 and c=3?

• If true for one pair of N0 and c, then there exists infinite set of such pairs of N0 and c

Big Oh Notation

• T(N) = O(f(N)) means it is guaranteed that T(n) grows at rate no faster than f(N) so f(N) is “Upper bound” of T(n)
• N^3 grows faster than N^2 so we may say that N^2 = O(N^3)

Example (2): Comparing Functions

• Which function is better?

10 n2 Vs n3

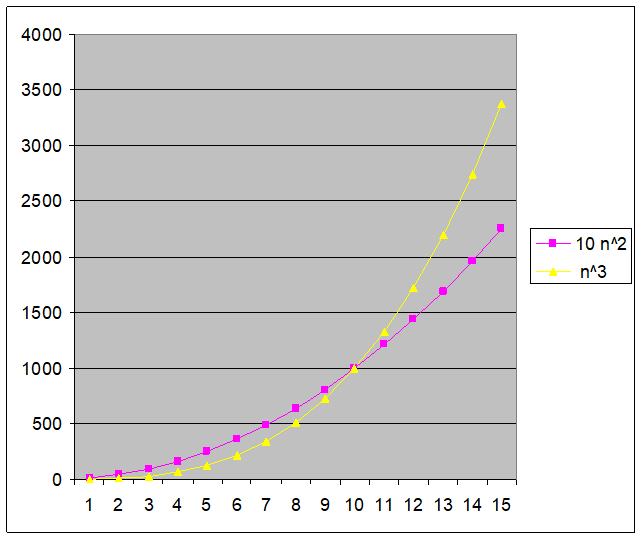
• As inputs get larger, any algorithm of a smaller order will be more efficient than an algorithm of a larger order

Big-Oh Notation

• Even though it is correct to say “7n – 3 is O(n3)”, a better statement is “7n – 3 is O(n)”, that is, one should make the approximation as tight as possible
• Simple Rule:

Drop lower order terms and constant factors

7n-3 is O(n)

8n2log n + 5n2 + n is O(n2log n)

Omega Notation

If f(N) and g(N) are two complexity functions, we say

f(N)  = W(g(N))

if there are constants c and N0 such that for N > N0,

f(N) >= c * g(N)

for all sufficiently large N.

Small Omega Notation

If f(N) and g(N) are two complexity functions, we say

f(N)  = W(g(N))

if there are constants c and N0 such that for N > N0,

f(N) > c * g(N)

for all sufficiently large N.

Theta Notation

If f(N) and g(N) are two complexity functions, we say

f(N)  = Q(g(N))

• c1 ´ f(n) is an Upper Bound on g(n)
• and c2 ´ f(n) is a Lower Bound on g(n)

Asymptotic notation

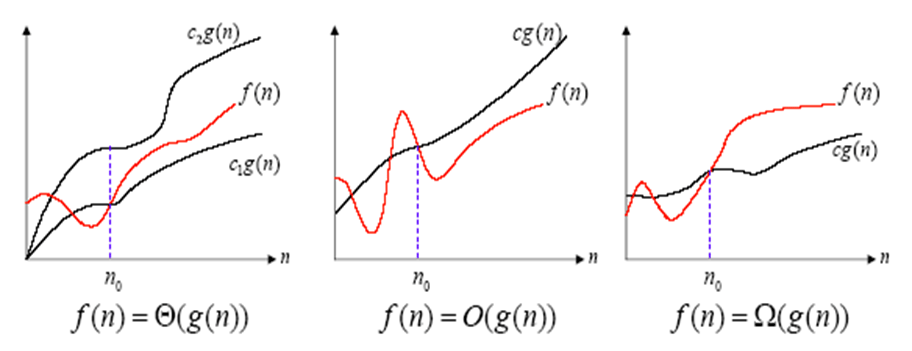
• Example:
• f(n) = 3n5+n4 = Q(n5)

Review of Three Common Sets

g(n) = O(f(n)) means c ´ f(n) is an Upper Bound on g(n)

g(n) = W(f(n)) means c ´ f(n) is a Lower Bound on g(n)

g(n) = Q(f(n)) means c1 ´ f(n) is an Upper Bound on g(n)

and  c2 ´ f(n) is a Lower Bound on g(n)

These bounds hold for all inputs beyond some threshold n0.

Some Questions

3n2 – 100n + 6 = O(n2)?

3n2 – 100n + 6 = O(n3)?

3n2 – 100n + 6 = O(n)?

3n2 – 100n + 6 = W(n2)?

3n2 – 100n + 6 = W(n3)?

3n2 – 100n + 6 = W(n)?

3n2 – 100n + 6 = Q(n2)?

3n2 – 100n + 6 = Q(n3)?

3n2 – 100n + 6 = Q(n)?

Performance Classification

Size does matter[1]

What happens if we double the input size N?

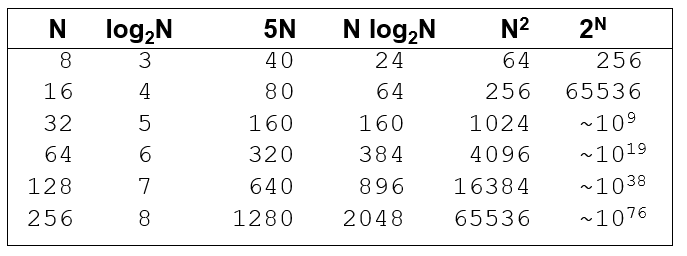
Size does matter[2]

• Suppose a program has run time O(n!) and the run time for

n  = 10 is 1 second

For n = 12, the run time is 2 minutes

For n = 14, the run time is 6 hours

For n = 16, the run time is 2 months

For n = 18, the run time is 50 years

For n = 20, the run time is 200 centuries