Theory of automata all previous/ past question papers
– Theory of automata project-Computer Science all subject past paper – Theory of automata Problem with source code – Theory of automata Course – Theory of automata Project idea – Theory of automata MCQ – Theory of automata Interview Question –Computer Science all courses – Theory of automata concepts-University Past Paper – Theory of automata-Question paper –old paper
Theory of automata final paper
Q.1
Convert this following game scenario into NFA and then convert this NFA into a regular
expression.
The game of Flips is played with three coins. Initially they are all heads. A move consists of
flipping. Two coins simultaneously from whatever they were to the opposite side. For example,
flipping the end coins changes THH into HHT. We win when all three coins are tails. There are
eight possible states: HHH, HHT …. TTT. The only – is HHH; the only + is TTT. Draw this NFA,
the shortest word in this language is the shortest solution of this puzzle. What is it? Also tell how
many moves are in each winning sequence.
Q.2
Even though a CFG is not in regular form it still might generate a regular language. If so, this
means that there is another CFG that defines the same language and is in regular form. For the
following CFG’s find regular expressions that define the same language and describe the
language
a)
S—-→ aS| bX| a
X–→ aX| bY| a
Y–→ aY| a
b)
S–> aS| bX| a
X— aX| bY| bZ| a
Y-> aY| a
Theory of automata Mid term in 2021
Q1: a) Compute and mention all the words of length 6 and 7 for the Languages B*, Where
B = {zo oz}
- b) Also find if the string “zoozzoozzoozozozo” belongs to B*.
Q2: Build an FA that accepts Your Registration Number. Clearly mention all the symbols included in the sigma to describe the strings of its language.
Q3: a) Construct (by Theorem) an equivalent DFA from the NFA given below:
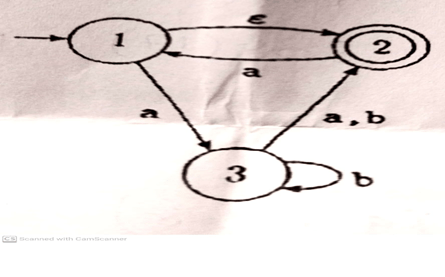
b) Show that the same DFA will be constructed by applying the Algorithm to the NFA shown above.
Q4: Find the RE of the NFA given in Q3.
Q5: Apply Thompsons construction method to build an FA of the RE stated below:
a (ba) * b(^+a) b
Theory of automata Final Paper in 2022
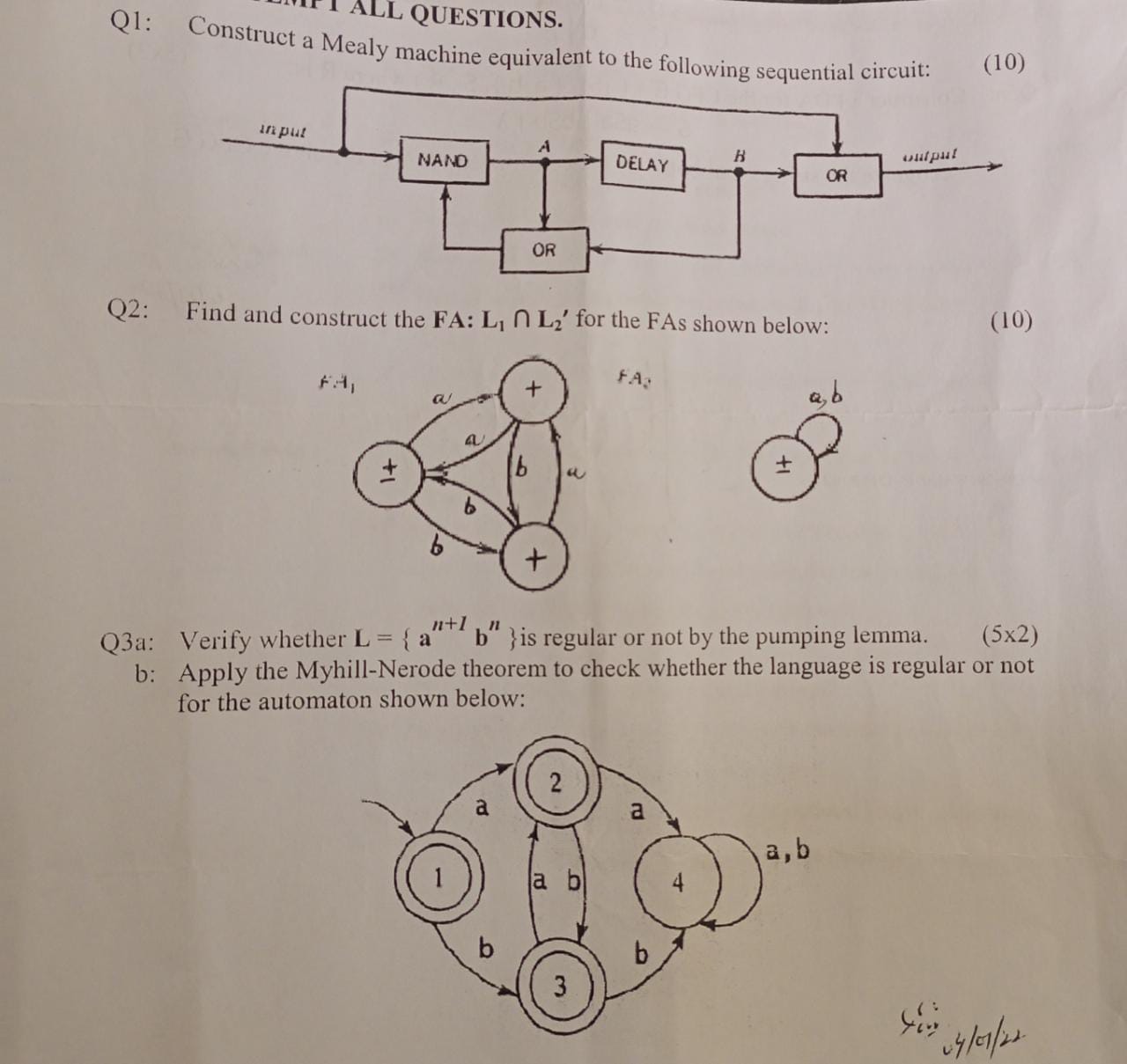

# Theory of automata project #Computer Science all subject past paper # Theory of automata Problem with source code # Theory of automata Course # Theory of automata Project idea # Theory of automata MCQ #Wireless & Theory of automata Interview Question #Computer Science all courses # Theory of automata #University Past Paper # Theory of automata #Question paper #old paper

