Numerical Computing all previous/ past question papers

– Numerical Computing-Computer Science all subject past paper Numerical Computing –Computer Graphics  Course  Numerical Computing Project idea – ICT  MCQ -Numerical Computing Interview Question  –Computer Science all courses -Technology –University Past Paper -Programming language –Question paper –old paper

Numerical Computing Fall 21 past paper

Numerical computing final paper

1. Solve the following system using Jacobi method (with 4 digu roues arithmetic, at least). Assume the error tolerance as 0.0001.

15x₁-2X2-6Xj+0x₁ -2x)+12×2-4X3-X4=300

0 -6×1-4×2+19×3-9×4 =0

0x1-X2-9X3+21x₁=0

(Marks 10)

2. Obtain the first and second derivative at x-7 using Stirling formula. Where

Xp= 12

X

5

6

7

8

9

10

f(x)

196

394

686

1090

1624

2306

(Marks-10)

x

3. Use the table in Question no. 2 of values by Newton forward differentiation formula. To compute f (0.25), (0.50), (0.75).

2125 (Marks= 15)

4. Use Question no. lequations, to find X1, X2, X3, and x, values using Gauss

Jordan Elimination Method.

(Marks 10)

5. Compute ff(x) dx based on Trapezoidal rule. 0.6

X

0

0.1

0.2

0.3

0.4

0.5

0.6

f(x)

0

0.0998

0.1987 0.2955 0.38994

0.4794

0.5646

(Marks-05)

Numerical Computing  Mid term paper

Q1:

Find the Error if found then remove that error?

x	F(x)
2.5	24.145
2.0	22.043
2.5	20.225
2.5	18.644
2.2	17.262
3.0	16.047

Q2:

Find the approximate value of following integral for step, h = 0.25

Over the interval [3,9] where f(x) = x/x+3.

1. Composite Bool’s rule
2. Composite Weddle’s rule

Q3:

Construct the Newton’s Forward difference interpolating polynomial passing through the points (-1,-3), (1, 5), (3, 17), and (5, 21).

paper 2

Q1:

It is suspected that there is an error in one of the values of f(x) in the following table:

X	0	1	2	3	4	5	6	7	8	9	10
f(x)	0	2	20	90	272	605	1332	2450	4160	6642	10100

Construct the differences-table, detect and correct the error.

Q2:

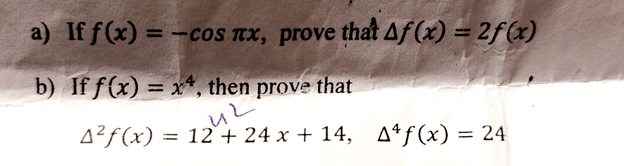
Q3:

The following table represents the time x and the corresponding velocity f(x) of the particle moving with non-uniform velocity.

X	0.0	1.0	1.5	2.0
f(x)	2.5	1.0	4.6	5.3

From this table, using Lagrange’s formula inversely, determine the time when the velocity of the particle becomes 2.75.

 

Numerical Computing Sessional 1 question paper

NC S1

Numerical Computing Sessional 2 question paper

1. Filling the blanks (Score: 2 5=10)

(1)     Let ξ=g(ξ)∈[a, b] be a fixed point of the real-valued and continuous function g(x). If g(x) has a continuous derivative in some neighborhood of ξ with ________.

Then the sequence (x_k) defined by x_k+1=g(x_k) converges to ξ as k→∞, provided that x₀ is sufficiently close to ξ.

(2)     Assume that .Let be distinct real numbers and suppose that are real numbers. Then, there exists a unique Lagrange polynomial such that ____________.

 

(3)     Suppose that a real-valued function g(x) has a fixed point ξ in [a, b]. Then, the corresponding expression can be written as________.

(4)     Given that 4x²-a=0, where a is positive real number. Then, the iteration for solving this equation by the secant method can be expressed as ____________with x₀ and x₁ being the starting values.

 

(5)     During the process of finding the single solution to the equation f(x) =0 in [a₀, b₀] with f(a₀)f(b₀)<0, the first step is to consider the midpoint . If (the given tolerance), then we need to choose the new interval:[a₁, b₁]=[a₀, c₀] in the case of _____;or [a₁, b₁]=[c₀, b₀] in the case of _____.

1. Find solution using Bessel’s formula Score= 10
2. Find Solution using Newton’s Backward Difference formula    Score=10

x	f(x)
3.5	34.145
4.0	32.043
4.5	30.225
5.0	28.644
5.5	27.262
6.0	26.047

x = 4.75

Numerical Computing Final question paper

1. MCQ’s (Marks=10)
   204. How much significant digits in this number 204.020050?
        1. 5
        2. 7

• 9

1. 11
2. In which of the following method, we approximate the curve of solution by the tangent in each interval.
   1. Hermite’s method
   2. Euler’s method

• Newton’s method

1. Lagrange’s method

 

1. When   do   we   apply   Lagrange’s   interpolation?
   1. Evenly spaced
   2. Unevenly spaced

• Both

1. None of above
2. When   Newton’s   backward formula is used?
   1. To interpolate values
   2. To calculate difference

• To find approximate error

1. None of above

 

1. What are the errors in Trapezoidal rule of numerical integration?
   1. E<Y
   2. E>Y

• E=Y

1. None of above

 

2. Consider the initial value problem; give the condition of the absolute stability for the Euler method. (Marks= 10)

 

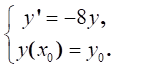
2. Suppose that the function values of f(x) are given in the following table.

X	-1	1	2
ln X	-3	0	4

(Marks= 10)
Find the approximate function value at the point  by the Lagrange’s interpolation polynomial of degree 2.

 

4. Use the predictor-corrector method to get the approximate solution of the following initial value problem (Marks= 10)

 

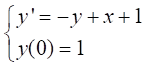            with h = 0.1, 0 < x < 0.5.

 

5. Consider the function f(x) = cos x−x=0. Approximate a root of f(x) via Newton’s Method. (Marks= 10)

Numerical Computing Final Paper 2022

 

#Numerical Computing #Computer Science all subject past paper  Numerical Computing #Computer Graphics  Course  #Numerical Computing Project idea  #Numerical Computing MCQ  #Numerical Computing  Interview Question  #Computer Science all courses #Technology #University Past Paper #Programming language  #Question paper  #old paper