Discrete Structures all previous/ past question papers
-Discrete Structures-Computer Science all subject past paper Discrete Structures –Computer Graphics Course – Discrete Structures Project idea -Discrete Structures MCQ -Discrete Structures Interview Question –Computer Science all courses -Technology –University Past Paper -Programming language –Question paper –old paper
Discrete Structures Sp22 Mid term paper

Midterm Exam 2021
Q1: Write down what it means for a relation to be transitive. Let A be the set{1,2,3} and the following relations are subsets of A x A. Which of the relations below are transitive? Give justification
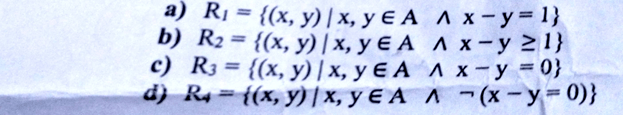
Q2: Prove or give a counterexample for each of the following:
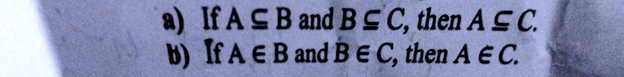
Q3:
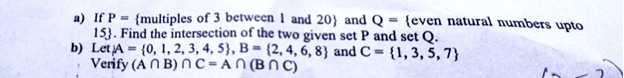
Q4:

Q5: Differentiate Between symmetric, anti-symmetric and asymmetric relations with suitable example.
Sessional 2 2020
Q 01: Fing the argument form for the following argument and determine whether it is valid Can we conclude that the conclusion is true if the premises are sure?
If Socrates is human, then Socrates is mortal. Socrates is human Socrates is mortal. (3)
Also verify the argument by using the truth table.
Q #02: Show, that the hypotheses “it is not sunny this afternoon and it is colder than yesterday.” we will go swimming only if it is sunny,” “if we donot go swimming then we will take a canoe trip” and “if we take a canoe trip the we will be home by sunset” leads to the conclusion “we will be home by sunset”. (3)
Q:#03:
- a) Check whether the following expressions are functions 1) Rx)=1/x 2) Rx)=x 3) f(x)=(x² + 1)¹²
- b) Determine whether each of these functions is a bijection from R to R. 1) f(x)=2x+1 2) f(x)=x²+1
c) Classify the functions given below whether these are one to one or ont or both

Q 04: Let A- (1, 2, 3, 4, 5), B- (5.6, 7) and C-(a, b) a) Find all the subsets of C.
- b) Find the power set of A.
- c) Whether A, B and C are disjoint sets? d) What is the cardinality of AUBUC
- e) What is the cardinality of A-B
GOOD LUCK
Final paper 2020
Qno.1:
A Construct the truth table of the compound proposition (PQ) — (P/Q) h Let P and Q be the Propositions where P: it is below freezing and Q: It is snowing, write the propositions using P. Q and logical
1) It is below freezing and snowing. connectives
2) It is below freezing but not snowing. 3) It is not below freezing and it is not snowing.
4) If it is below freezing, it is also snowing.
5) It is either below freezing or it is snowing, but it is not snowing if it is below freezing State which rule of inference is used in this argument if it rains today then we will not have a barbecue today. If we do not have a barbecue today then we will have a barbecue tomorrow. Therefore it it rains today then we will have a barbecue tomorrow. d) Use rule of inference to show that the hypotheses “Randy works hard” “If randy works hard, then he is a dull boy” and “If Randy is a dull boy, then he will not get a job” imply the conclusion “Randy will not get the job”.
1 102 10
#02: 10 Marks192679
- a) Determine whether is a function from to Rif 1) f(n)-1/n. 2) f(n) +(²+1)
3) f(n) 1/(n²-4)
- b) what is the value of 1-1
- c) By using Mathematical induction show that if n is a positive integer then
1+2++n=”2
Q03: 12 Marks(8+4)
- A) Describe an algorithm for the multiplication of two matrices of arbitrary order. b) Discuss the time complexity of linear search algorithm.
#104: 5 Marks(2+3)
- The chain of an auditorium are tobe laheled with a letter and a positive integer not exceeding 100. What is the largest number of chairs that can be labeled differently? b) What is the value of K after the following code has been executed? Code on the next page.
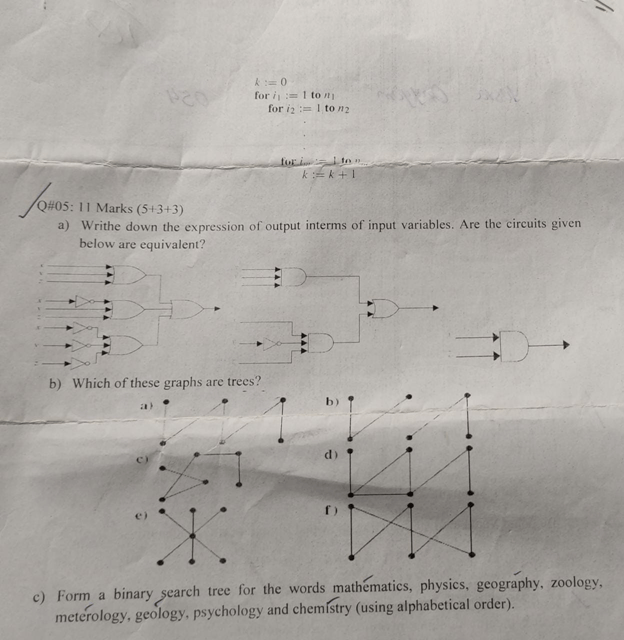
Sessional 1 2020
Q NO 1:
(a) Define set equality, reflexive relation, function, statement, rule and argument.
(b) Construct the truth table for the An (BUC)=(ANB)U(ANC) to convert into logical form.
Q NO 2:
(a) Prove that (An B) = AC U B through venn diagram, if set A is subset of set 8.
(b) Use truth table to determine the argument form
p–>q
p–>r
p^q
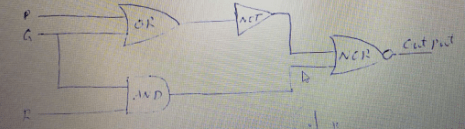
(c) Indicate all ouputs of a circuit given below using all possible input signals.
Sessional 2 2020
Q NO 1:
(a) Define even numbers and composite numbers. (1+2+2)
(b) Ler Q(n) be the predicate “n is a factor of 8”
Find the tuth set of Q(n) if the domain of n is the set 2′ of all positive integers.
(c) Suppose that r and s are integers.
Prove that there exist an integer k such that 22r+18s-2k
Q NO 2: (2+2+2+4)
(a) Find an explicit formula to fit given initial terms
1, 4’9’16’25’ 36
(b) State and explain pigeonhole principle.
(c) Let A = (1,2,3,4,5,6,7,8) if five integers sre selected fromA, must atleast one pair of integers have a sum of 9?
(d) For ax inetgers n 20,22-1 is divisible by 3 (prove by mathematical induction)


