Time Complexity of Algorithms
Ultimate goal of Algorithm Design is to complete tasks efficiently.
What does “efficiently” means ?
Efficiency depends upon Running Time.
Running Time of Algorithm
What effects running time of an algorithm?
(a) computer used, the hardware platform (Single Processor / Multi- Processor , Computer Generation , 32bit / 64 bit etc.)
(b) Memory Read / Write Speed and Type (Sequential , Random, Indexed)
(c) Compiler / Interpreter efficiency.
(d) Programming Skills
(e) Complexity of underlying algorithm
(f) Size of the input
Most Important factors are (e) and (f).
Algorithm Analysis means
To analyze an algorithm means:
developing a formula for predicting how fast an algorithm is, based on the size of the input (time complexity), and/or
developing a formula for predicting how much memory an algorithm requires, based on the size of the input (space complexity)
SO, Efficiency is measured in terms of Time and Space which is also known as
COMPLEXITY OF ALGORITHM
Complexity of Algorithm
- Complexity of an algorithm is a measure of the amount of time and/or space required by an algorithm for an input of a given size (n).
- Analysis of Algorithm depends on
–How good is the algorithm?
- Correctness
- Time Efficiency
- Space Efficiency
–Does there exist a better algorithm?
- Lower bounds
- Optimality
Algorithm Design Techniques
- Brute force
- Divide and conquer
- Decrease and conquer
- Transform and conquer
- Greedy approach
- Dynamic programming
- Backtracking and branch-and-bound
- Space and time tradeoffs
Time Complexity of Algorithm
Rate of Growth
Rate of growth is the rate at which running time increases as a function of input.
Lower Order Term
When given an approximation of the rate of growth of a function, we tends to drop the lower order terms as they are less significant to higher order terms.
e.g f(n) = n2 + n
Lower order term n will be dropped and
O(n2)
Here what is O (Oh)?
We can analyze algorithms in one of 3 ways
Worst Case
Longest Time
Represented by O (Big- Oh)
Best Case
Least Time
Represented by Ω (Big – Omega)
Average Case
Average Time
Represented by Φ(Big – Theta)
These are known as Asymptotic Notations Asymptotic notation of an algorithm is a mathematical representation of its complexity
Time Complexity of Algorithm
Big – Oh Notation (O)
- Big – Oh notation is used to define the upper bound of an algorithm in terms of Time Complexity.
- Worst Case
Big – Omege Notation (Ω)
- Big – Omega notation is used to define the lower bound of an algorithm in terms of Time Complexity.
- Best Case
Big – Theta Notation (Θ)
- Big – Theta notation is used to define the average bound of an algorithm in terms of Time Complexity.
- Average Case
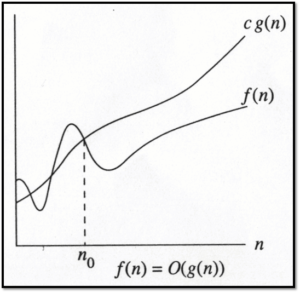
The idea is to establish a relative order among functions for large
n $ c , n0 > 0 such that
f(n) £ c g(n)
when n ³ n0
f(n) grows no faster than g(n) for “large” n
Asymptotic notation: Big-Oh
f(n) = O(g(n))
There are positive constants c and n0 such that
f(n) £ c g(n) when n ³ n0
The growth rate of f(n) is less than or equal to the growth rate of g(n), so g(n) is called an upper bound on f(n)
Time Complexity
Execution Time Taken by Your Program.
Example: Consider the following program and judge how much time it will take to execute.
main( )
{
x = y + z; 1 statement takes 1 time
}
So Time Complexity of the program is O(1)
here O is known as BIG Oh
Note: All pre-define functions like +, -, *, scanf, printf etc will take constant time to execute.
main( )
{
x = y + z; 1 statement takes 1 time
for(i=1;i<=n;i++) loop takes n time to execute
{
a = b + c;
}
}
Total Complexity is O(n+1) è O(n)
This program will take maximum n+1 time. Here O is known as Big-Oh which is currently considered as one of the unit of Time Complexity.
main()
{
x = y + z; O(1) // 1 statement take 1 time only
for(i=1;i<=n;i++) O(n) // This loop takes n time to execute
{
for(j=1;j<=n;j++) O(n) This loop take n time to execute
{
a = b + c;
}
}
}
Total Time Taken by this code is n x n times => O(n2)
The Whole program complexity is O(n2 + 1) è O(n2)
main()
{
While( n >= 1)
{
n = n – 1; it execute n time O(n)
n = n – 2; it execute n/2 time = O( n / 2)
n = n – 20; it executes n/20 time = O(n/20)
}
}
…………………
main()
{
While( n >= 1)
{
n = n / 2; It takes log 2 n times to execute
}
}
The Whole program complexity is O(log 2 n )
Every time value of n decreases until a value came which will stop the loop.
Like as
n/2 n/22 n/24 n/26 ………………………….- n/2k
Explanation
Every time value of n decreases until a value came which will stop the loop.
Like as
n/2 n/22 n/24 n/26 ………………………….- n/2k
So we can write n / 2K = 1
2K = n
k = log 2 n
Time Complexity is O(log 2 n )
PROOF:
Lets consider n = 128
Loop Executes as 128 64 32 16 8 4 2 1 (STOP)
Loop Executed 7 times
Lets check Log2 n = Log2 128 n = (27 = 128) = 7
………………..
main()
{
While( n <= 2)
{
n = √n;
}
}
Explanation
How many times the above program executes
√n = (n)1/2 n1/2 n1/4 n1/6 n1/8 …………….. n1/2k
1/2k log 2 n = 1
log 2 n = 2k
log (log 2 n ) = k
………………..
main()
{
While( a <= n)
{
a = a + 1; O(n)
a = a + 20; O( n / 20)
a = 2 * a; O(log 2 n)
a = a * a; O(log 2 log 2 n)
a = a 2 ; O(log log 2 n)
}
}
……………
main()
{
for(i=1;i<=n;i++) O(n)
{
for(j=1;j<=n;ij = 2 * j) O(log 2 n)
{
x = y + z;
}
}
}
Time Complexity O(n log 2 n)
………………….
main()
{
for(i=1;i<=n;i++) ( n)
{
j = 2;
while ( j <= n)
{
j = j 2; log (log 2 n)
}
}
}
Time Complexity O(n log ( log 2 n) )
…………………..
main()
{
for(i=1;i<=n;i++)
{ for(j=1;j<=I;j++)
{ for(k=1;k<=n;k++) {
x = y + z; } }}
}
Explanation
i 1 2 3 … (n + 2n + 3n + ….. nn)
j 1 1,2 1,2,3 … n(1 + 2 + 3 …….. n)
k n 2n 3n … n ( n (n +1) /2)
O(n3)
……………………..
main()
{
for(i=1;i<=n;i++)
{ for(j=1;j<=I;j++)
{ for(k=1;k<=n;k=k2) {
x = y + z; } }}
}
Explanation
i 1 2 3 …
j 1 1,2 1,2,3 …
k log (log 2 n) 2 log (log 2 n) 3 log (log 2 n)
log (log 2 n) (1 + 2 + 3 + ….. n)
O(n2 log (log 2 n))

