BFS pseudocode

The pseudocode for BFS in python goes as below:

create a queue Q

mark v as visited and put v into Q while Q is non-empty

remove the head u of Q

mark and enqueue all (unvisited) neighbors of u

BFS implementation in Python (Source Code)

Now, we will see how the source code of the program for implementing breadth first search in python.

Consider the following graph which is implemented in the code below:

graph = {

‘5’ : [‘3′,’7’],

‘3’ : [‘2’, ‘4’],

‘7’ : [‘8’],

‘2’ : [],

‘4’ : [‘8’],

‘8’ : []

}

visited = [] # List for visited nodes.

queue = []     #Initialize a queue

def bfs(visited, graph, node): #function for BFS

visited.append(node) queue.append(node)

while queue:

m = queue.pop(0)

print (m, end = ” “)

for neighbour in graph[m]:

if neighbour not in visited: visited.append(neighbour) queue.append(neighbour)

# Driver Code

print(“Following is the Breadth-First Search”)

bfs(visited, graph, ‘5’)    # function calling

In the above code, first, we will create the graph for which we will use the breadth-first search. After creation, we will create two lists, one to store the visited node of the graph and another one for storing the nodes in the queue.

After the above process, we will declare a function with the parameters as visited nodes, the graph itself and the node respectively. And inside a function, we will keep appending the visited and queue lists.

Then we will run the while loop for the queue for visiting the nodes and then will remove the same node and print it as it is visited.

At last, we will run the for loop to check the not visited nodes and then append the same from the visited and queue list.

As the driver code, we will call the user to define the bfs function with the first node we wish to visit.

Output

The output of the above code will be as follow:

Following is the Breadth-First Search    5 3 7 2 4 8

Example

Let us see how this algorithm works with an example. Here, we will use an undirected graph with 5 vertices.

We begin from the vertex P, the BFS algorithmic program starts by putting it within the Visited list and puts all its adjacent vertices within the stack.

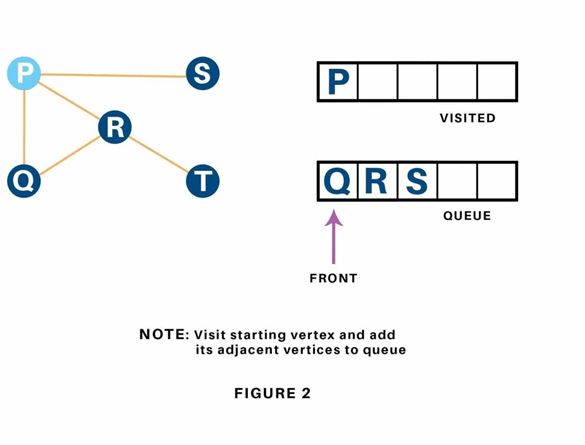
Next, we have a tendency to visit the part at the front of the queue i.e. Q and visit its adjacent nodes. Since P has already been visited, we have a tendency to visit R instead.

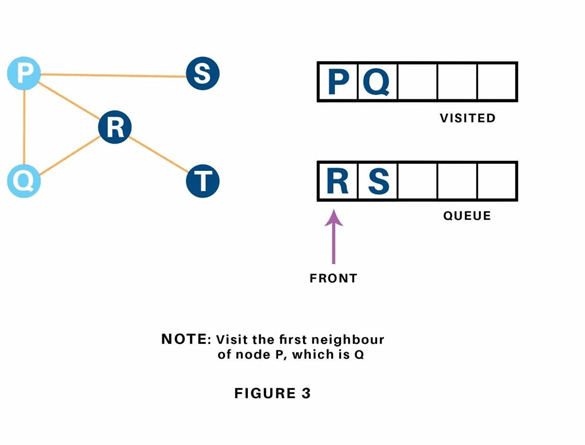
Vertex R has an unvisited adjacent vertex in T, thus we have a tendency to add that to the rear of the queue and visit S, which is at the front of the queue.

Now, only T remains within the queue since the only adjacent node of S i.e. P is already visited. We have a tendency to visit it.

Since the queue is empty, we’ve completed the Traversal of the graph.