Lab5

Activity Outcomes:

This lab teaches you the following topics:

• How to represent problems in terms of state space graph
• How to find a solution of those problems using A* search.
• How to find a solution of those problems using hill climbing.

Introduction:

So far we have studied uninformed search strategies. There can also be occasions where we are given some extra information related to a particular goal in the form of heuristics. We can use such heuristics in our search strategy. A particular form of this strategy known as A* search uses the total cost of a solution via a particular node as that node’s evaluation criteria. We will see its implementation in detail. We will also see hill climbing which is an instance of local search strategy.

Lab Activities:

Activity 1:

Consider a maze as shown below. Each empty tile represents a separate node in the graph, while the walls are represented by blue tiles. Your starting node is A and the goal is to reach Y. Implement an A* search to find the resulting path.

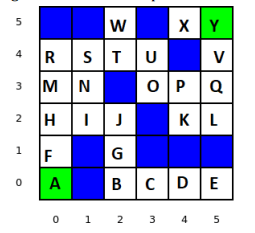
Solution:

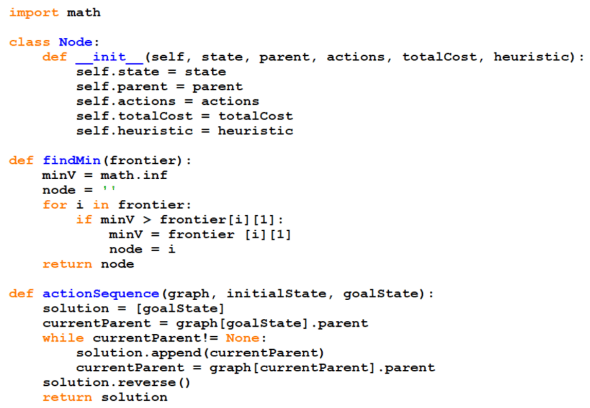
Since A* search needs a heuristic function that specifies the distance of each node with the goal, you can use Euclidean distance between a particular node and the goal node as your heuristic function of that particular node.

But first we need to modify the structure of Node class that will also include the heuristic distance of that node.

Next we modify the structure of dictionary that will save our graph. Here at each node, we also specify the coordinate location of each node. For implementation we will follow uniform cost implementation except for the fact that the total cost will include both the previous cost of reaching that node and the distance of the goal with that node.

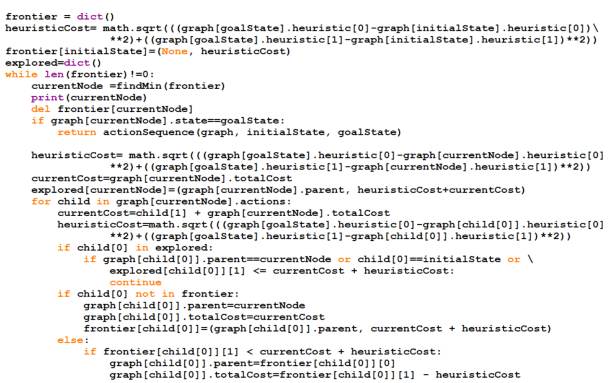
Activity 2:

For the graph in previous activity, imagine node A as starting node and your goal is to reach Y. Apply hill climbing and see how closer you can get to your destination.

Solution:

Instead of maintaining a fringe or a frontier to save the nodes that are to be explored, hill climbing just explores the best child of a given node, then explores the best grandchild of a particular child and so on and so forth.

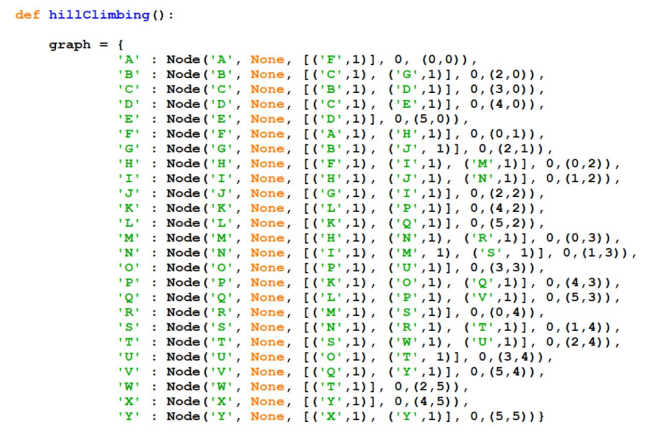
This will give [‘F’, ‘H’, ‘I’, ‘J’] as the solution, which means that the algorithm gets stuck at J and doesn’t go further towards Y since the distance of G is greater than J.
Remember that the path is not important in local search. The solution should be your last node (currently that is J which happens to be local maxima).

Home Activities:

Activity 1:

Since hill climbing can get stuck as a local minima as we saw in the previous activity, apply random restart hill climbing to get to your goal Y. How many restarts do you need in this case?

Assignment:

To the same maze, apply local beam search to reach to your goal Y. Show parent and children nodes at each iteration.